Bài 5:
a) \(x^2-7x+6=x^2-x-6x+6=\left(x^2-x\right)-\left(6x-6\right)=x\left(x-1\right)-6\left(x-1\right)=\left(x-1\right)\left(x-6\right)\)
b) \(x^2+12x+35=x^2+7x+5x+35=\left(x^2+7x\right)+\left(5x+35\right)=x\left(x+7\right)+5\left(x+7\right)=\left(x+7\right)\left(x+5\right)\)
c) \(x^2-x-56=x^2-8x+7x-56=\left(x^2-8x\right)+\left(7x-56\right)=x\left(x-8\right)+7\left(x-8\right)=\left(x-8\right)\left(x+7\right)\)
d) \(5x^2-x-4=5x^2+4x-5x-4=\left(5x^2+4x\right)-\left(5x+4\right)=x\left(5x+4\right)-\left(5x+4\right)=\left(5x+4\right)\left(x-1\right)\)
e) \(x^4+64=x^4+16x^2+64-16x^2=\left[\left(x^2\right)^2+2\cdot x\cdot8+8^2\right]-\left(4x\right)^2=\left(x^2+8\right)^2-\left(4x\right)^2=\left(x^2-4x+8\right)\left(x^2+4x+8\right)\)
g) \(4x^4+1=4x^4+4x^2+1-4x^2=\left(2x^2+1\right)^2-\left(2x\right)^2=\left(2x^2-2x+1\right)\left(2x^2+2x+1\right)\)
h) như ý g
i) Thêm bớt: \(16x^2y^2\)
Câu 6,7,9: Ptđt thành nhân tử rồi tìm x, hoặc tính nhé! (3 bài này dụng phương pháp đặt nhân tử chung , dùng hđt , or nhóm nhé!)
Bài 8:
a) \(A=x^2-4x+10=x^2-4x+4+6=\left(x-2\right)^2+6\ge6\)
=> \(A_{min}=6\) khi \(x-2=0\Rightarrow x=2\)
b) \(B=x^2-2x+5=x^2-2x+1+4=\left(x-1\right)^2+4\ge4\)
=> \(B_{min}=4\) khi \(x-1=0\Rightarrow x=1\)
bài 5)
a) x2 - 7x + 6
= x2 - x - 6x + 6
= x(x - 1) - 6(x - 1)
= (x - 6)(x - 1)
b) x2 + 12x + 35
= x2 + 5x + 7x + 35
= x(x + 5) + 7(x + 5)
= (x + 7)(x + 5)
c) x2 - x - 56
= x2 - 8x + 7x - 56
= x(x - 8) + 7(x - 8)
= (x + 7)(x - 8)
d) 5x2 - x - 4
= 5x2 - 5x + 4x - 4
= 5x(x - 1) + 4(x - 1)
=(5x + 4)(x - 1)
e) x4 + 64
= x4 - 16x2 + 64 + 16x2
= [x4 - (4x)2] + (16x2 + 64)
= (x2 + 4x)(x2 - 4x) + 16(x2 + 4)
= (x2 + 4)(x2 - 4x + 16)
g) 4x4 + 1
= (4x4 + 4x2 + 1) - 4x2
= (2x2 + 1) - 4x2
= (2x2 + 1 - 2x)(2x2 + 1 + 2x)
h) 4x4 + 81
= (4x4 + 36x2 + 81) - 36x2
= (2x2 + 9)2 - 36x2
= (2x2 + 9 + 6x)(2x2 + 9 -6x)
i) 64x4 + y4
= 64x4 + 16x2y2 + y4 - 16x2y2
= (8x2 + y2) - (4xy)2
= (8x2 + y2 - 4xy)(8x2 + y2 + 4xy)
bài 7)
a) xy + y2 - x - y
= (xy + y2) - (x + y)
= y(x + y) - (x + y)
= (y - 1)(x + y)
b) 25 - x2 + 2xy - y2
= 25 - (x2 - 2xy + y2)
= 52 - (x - y)2
= (5 - x + y)(5 + x - y)
bài 8)
A= x2 - 4x + 10
= x2 - 4x + 4 + 6
= (x - 2)2 + 6
vì (x - 2)2 \(\ge\)0 \(\forall x\in R\)
\(\Rightarrow\) (x - 2)2 + 6 \(\ge\) \(\forall x\in R\)
vậy GTNN của A= 6 tại x = 2
B = x2 - 2x + 5
= x2 - 2x + 1 + 4
= (x - 1)2 + 4
vì (x - 1)2 \(\ge\) 0 \(\forall x\in R\)
\(\Rightarrow\) (x - 1)2 + 4 \(\ge\) 0 \(\forall x\in R\)
vậy GTNN của B = 4 tại x = 1
bài 9)
x2 - 2xy - 9z2 + y2
= (x2 - 2xy + y2) - 9z2
= (x - y)2 - 9z2
= (x - y - 3z)(x - y + 3z)
thay x = 6; y = -4 và z = 30 vào biểu thức đại số, ta có:
(6 + 4 - 3.30)(6 + 4 + 3.30)
= -80.100
= -8000
tik cho mik nha vì bài 6 dài quá nên mik ko làm đâu, lười đánh máy lắm
Câu 8 : Tìm giá trị nhỏ nhất của đa thức sau :
a) \(A=x^2-4x+10\)
\(A=\left(x^2-2.x.2+2^2\right)+6\)
\(A=\left(x-2\right)^2+6\)
Nx: \(\left(x-2\right)^2\ge0\) với mọi x
\(\Rightarrow\left(x-2\right)^2+6\ge6\) với mọi x
\(\Rightarrow A\ge6\)
Vậy GTNN của biểu thức A là 6 đạt được khi :
\(\left(x-2\right)^2=0\)
\(\Rightarrow x-2=0\)
\(\Rightarrow x=2\)
b) \(B=x^2-2x+5\)
\(B=\left[x^2-2.x.\dfrac{1}{2}+\left(\dfrac{1}{2}\right)^2\right]+\dfrac{19}{4}\)
\(B=\left(x+\dfrac{1}{2}\right)^2+\dfrac{19}{4}\)
Nx : \(\left(x+\dfrac{1}{2}\right)^2\ge0\) với mọi x
\(\Rightarrow\left(x+\dfrac{1}{2}\right)^2+\dfrac{19}{4}\ge\dfrac{19}{4}\) với mọi x
\(\Rightarrow B\ge\dfrac{19}{4}\)
Vậy GTNN của biểu thức B là \(\dfrac{19}{4}\) đạt được khi :
\(\left(x+\dfrac{1}{2}\right)^2=0\)
\(\Rightarrow x+\dfrac{1}{2}=0\)
\(\Rightarrow x=-\dfrac{1}{2}\)
Làm lại câu b) bài 8 :
b) \(B=x^2-2x+5\)
\(B=\left(x^2-2.x.1+1^2\right)+4\)
\(B=\left(x-1\right)^2+4\)
Nx : \(\left(x-1\right)^2\ge0\) với mọi x
\(\Rightarrow\left(x-1\right)^2+4\ge4\) với mọi x
\(\Rightarrow B\ge4\) với mọi x
Vậy GTNN của biểu thức B bằng 4 đạt được khi :
\(\left(x-1\right)^2=0\)
\(\Rightarrow x-1=0\)
\(\Rightarrow x=1\)
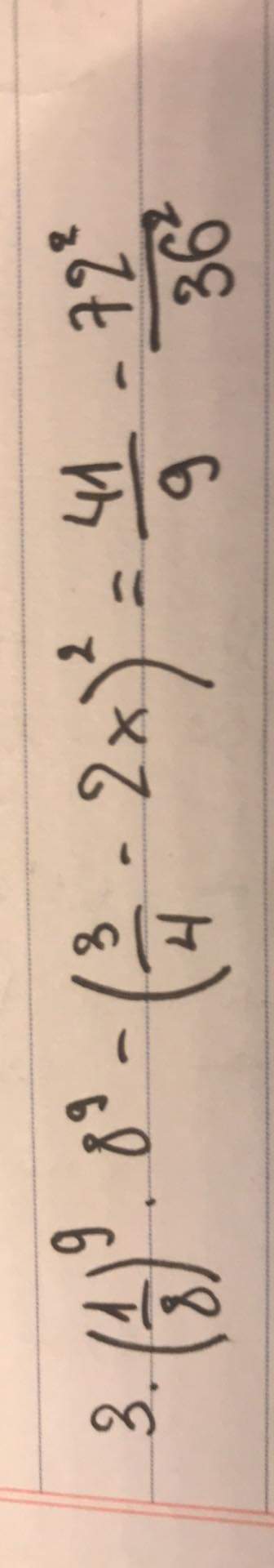
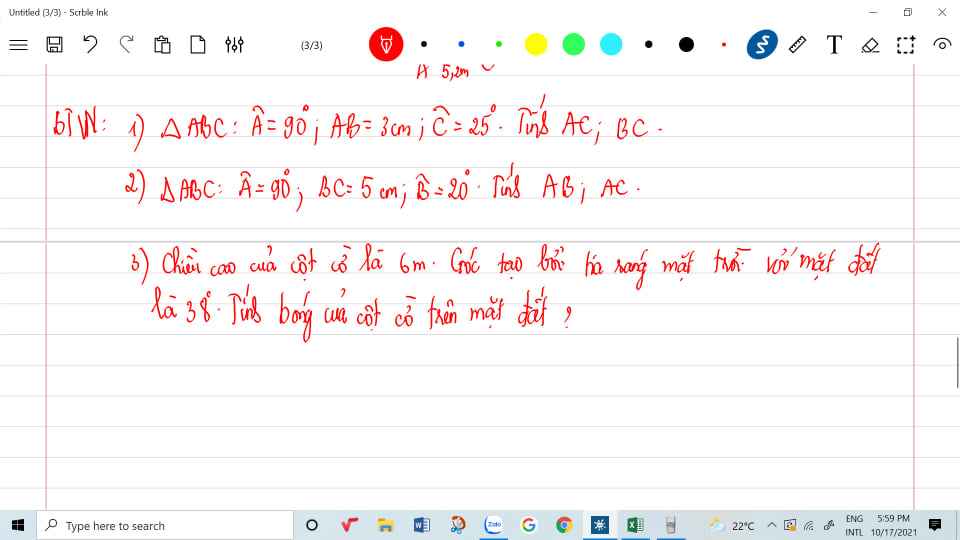Giúp mình với ạ mình cần gấp
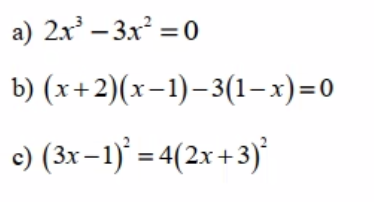
bài 2 câu 1,2,3,5,9 
