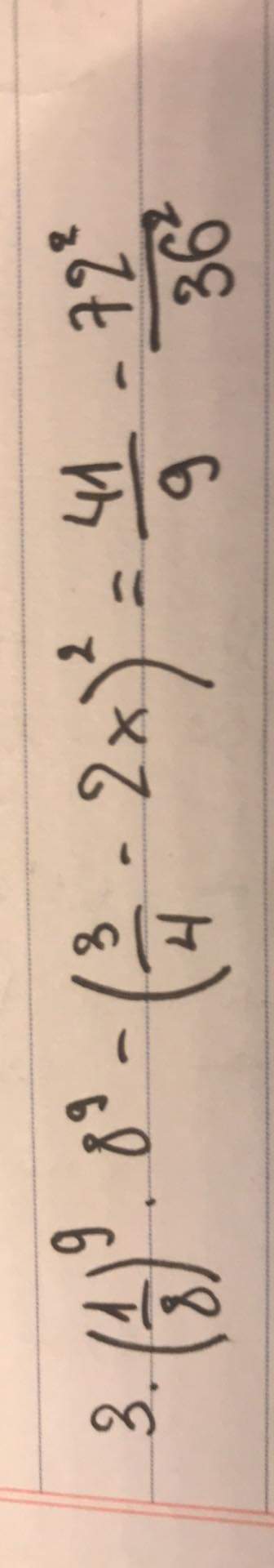\(\left(\dfrac{1}{8}\right)^9\cdot8^9-\left(\dfrac{3}{4}-2x\right)^2=\dfrac{41}{9}-\dfrac{72^2}{36^2}\\ \Rightarrow\left(\dfrac{1}{8}\cdot8\right)^9-\left(\dfrac{3}{4}-2x\right)^2=\dfrac{41}{9}-\left(\dfrac{72}{36}\right)^2\\ \Rightarrow1^9-\left(\dfrac{3}{4}-2x\right)^2=\dfrac{41}{9}-2^2=\dfrac{5}{9}\\ \Rightarrow\left(\dfrac{3}{4}-2x\right)^2=1-\dfrac{5}{9}=\dfrac{4}{9}\\ \Rightarrow\left[{}\begin{matrix}\dfrac{3}{4}-2x=\dfrac{2}{3}\\2x-\dfrac{3}{4}=\dfrac{2}{3}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}2x=\dfrac{1}{12}\\2x=\dfrac{17}{12}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=\dfrac{1}{24}\\x=\dfrac{17}{24}\end{matrix}\right.\)
Phép nhân và phép chia các đa thức
Đúng 1
Bình luận (0)
Các câu hỏi tương tự
b. tìm x bt 3x^2 -3x(x-2)=36
mn đại lượng giúp misha giải CHI TIẾT bài này nhé^^
thanks mn nhiều lắm^^
tính nhanh
a.x^2 +12x+36 tại x=94
mn đại lượng giúp misha giải CHI TIẾT bài này với^^
thanks mn nhiều lắm^^
làm giúp mình câu tìm x này với ạ.
(x+1)^3-(x-1)(x^2+x+1)-2=0
Giúp mình câu b bài 2 với mn ơi:3 mn trình bày đầy đủ phép tính ra hộ mình nhé. Mình cảm ơn nhiều!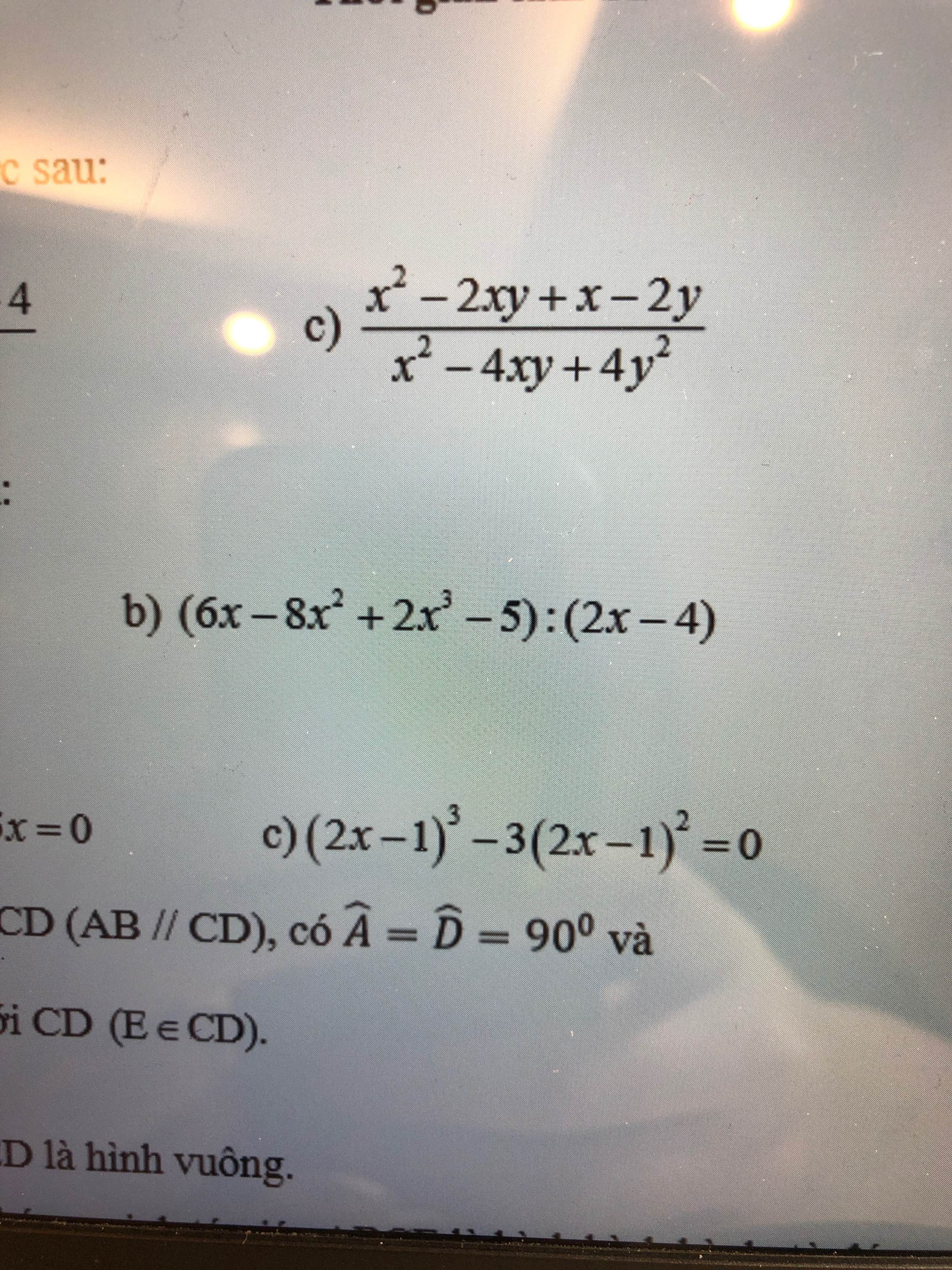
2 . ( x³ -1)-2x²(x+2x⁴) +(4x⁵+4)x=6. 3. (X²-4x+16)(x+4)-x(x+1)(x+2)+3x²= 0 4 . ( 8x +2 ) (1-3x) + ( 6x-1)(4x-10) =-50 Đề bài là tìm x nha mn Nhanh giúp mik vs
a.tìm x bt 3x+2(5-x)=0
mn đại lượng giúp misha giải CHI TIẾT bài này nhé^^
thanks mn nhiều lắm^^
Giúp dùm mình bài này với ạ
c/m g.trị của b.thức ko phụ thuộc vào g.trị của biến
a.x(3x+12)-(7x-20)+x^2 (2x-3)-x(2x^2 +5)
mn đại lượng giúp misha giải CHI TIẾT bài này nhé^^
thanks mn nhiều lắm^^
áp dụng hằng đẳng thức đáng nhớ tìm x biết:
(x+1)(x+2)-(x-3)^2=11
mấy bạn địa lượng giúp misha giải CHI TIẾT bài này với ,thanks mấy bạn nhiều ^^