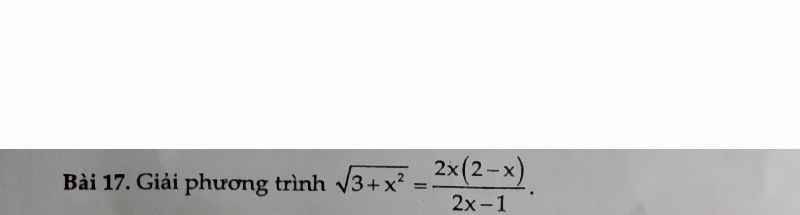Question

Giúp mình với

Answer 1

\(\Rightarrow\left(x+\sqrt{x^2+1}\right)\left(y+\sqrt{y^2+1}\right)=1\)

\(\Rightarrow\)\(\left\{{}\begin{matrix}-\left(y+\sqrt{y^2+1}\right)=x-\sqrt{x^2+1}\\-\left(x+\sqrt{x^2+1}\right)=y-\sqrt{y^2+1}\end{matrix}\right.\)(Nhân liên hợp rồi rút gọn)

Cộng 2 vế lại rồi rút gọn ta được: \(2\left(x+y\right)=0\Rightarrow x+y=0\Rightarrow x=-y\Rightarrow x^{2017}+y^{2017}=0\)