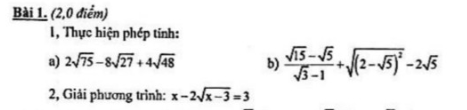Bài 1:
a: \(=10\sqrt{3}-24\sqrt{3}+16\sqrt{3}=2\sqrt{3}\)
\(1,\\ a,=10\sqrt{3}-24\sqrt{3}+16\sqrt{3}=2\sqrt{3}\\ b,=\dfrac{\sqrt{5}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}+\left|2-\sqrt{5}\right|-2\sqrt{5}\\ =\sqrt{5}+\sqrt{5}-2-2\sqrt{5}=-2\\ 2,ĐK:x\ge3\\ PT\Leftrightarrow\left(x-3\right)-2\sqrt{x-3}=0\\ \Leftrightarrow\sqrt{x-3}\left(\sqrt{x-3}-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-3=0\\\sqrt{x-3}=2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\left(tm\right)\\x=7\left(tm\right)\end{matrix}\right.\)
Bài 1:
\(a,2\sqrt{75}-8\sqrt{27}+4\sqrt{48}=10\sqrt{3}-24\sqrt{3}+16\sqrt{3}=2\sqrt{3}\\ b,\dfrac{\sqrt{15}-\sqrt{5}}{\sqrt{3}-1}+\sqrt{\left(2-\sqrt{5}\right)^2}-2\sqrt{5}=\dfrac{\sqrt{5}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}+\sqrt{5}-2-2\sqrt{5}=\sqrt{5}-\sqrt{5}-2=-2\)
Bài 2:
ĐKXĐ:\(x\ge3\)
\(x-2\sqrt{x-3}=3\\ \Leftrightarrow2\sqrt{x-3}=x-3\\ \Leftrightarrow4x-12=x^2-6x+9\\ \Leftrightarrow x^2-10x+21=0\\ \Leftrightarrow\left(x-3\right)\left(x-7\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=3\left(tm\right)\\x=7\left(tm\right)\end{matrix}\right.\)