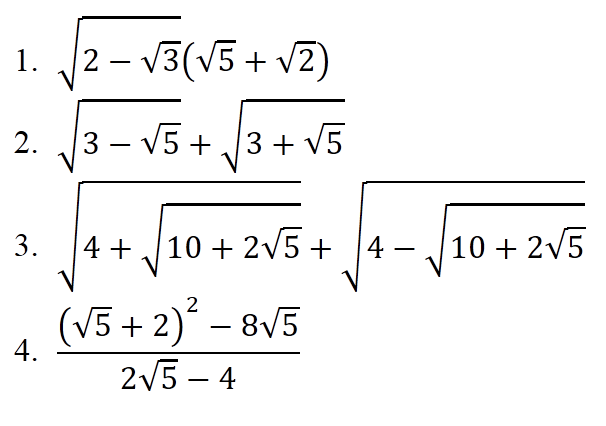Question

Giúp mình với ạ, mình đag cần GẤP lắm T-T

Cảm ơn nhiều nhiều ạ <3

 

Answer 1

Q = \(\dfrac{3\sqrt{x}}{x+1}\) (x \(\ge\) 0; x \(\ne\) 4)

Áp dụng BĐT Cô-si cho 2 số không âm x và 1 ta được:

\(\dfrac{x+1}{2}\ge\sqrt{x}\) (1)

\(\Leftrightarrow\) \(\dfrac{3\cdot\dfrac{x+1}{2}}{x+1}\ge\dfrac{3\sqrt{x}}{x+1}\) (x + 1 > 0 với mọi x \(\ge\) 0)

\(\Leftrightarrow\) \(\dfrac{6}{2\left(x+1\right)}\ge\dfrac{3\sqrt{x}}{x+1}\)

\(\Leftrightarrow\) \(\dfrac{3}{x+1}\ge\dfrac{3\sqrt{x}}{x+1}\) (*)

Dấu "=" xảy ra \(\Leftrightarrow\) x = 1 (TM)

Khi đó: \(\dfrac{3\sqrt{x}}{x+1}\le\dfrac{3}{1+1}=\dfrac{3}{2}\)

Vậy Q_Max = \(\dfrac{3}{2}\) khi và chỉ khi x = 1

Chúc bn học tốt!