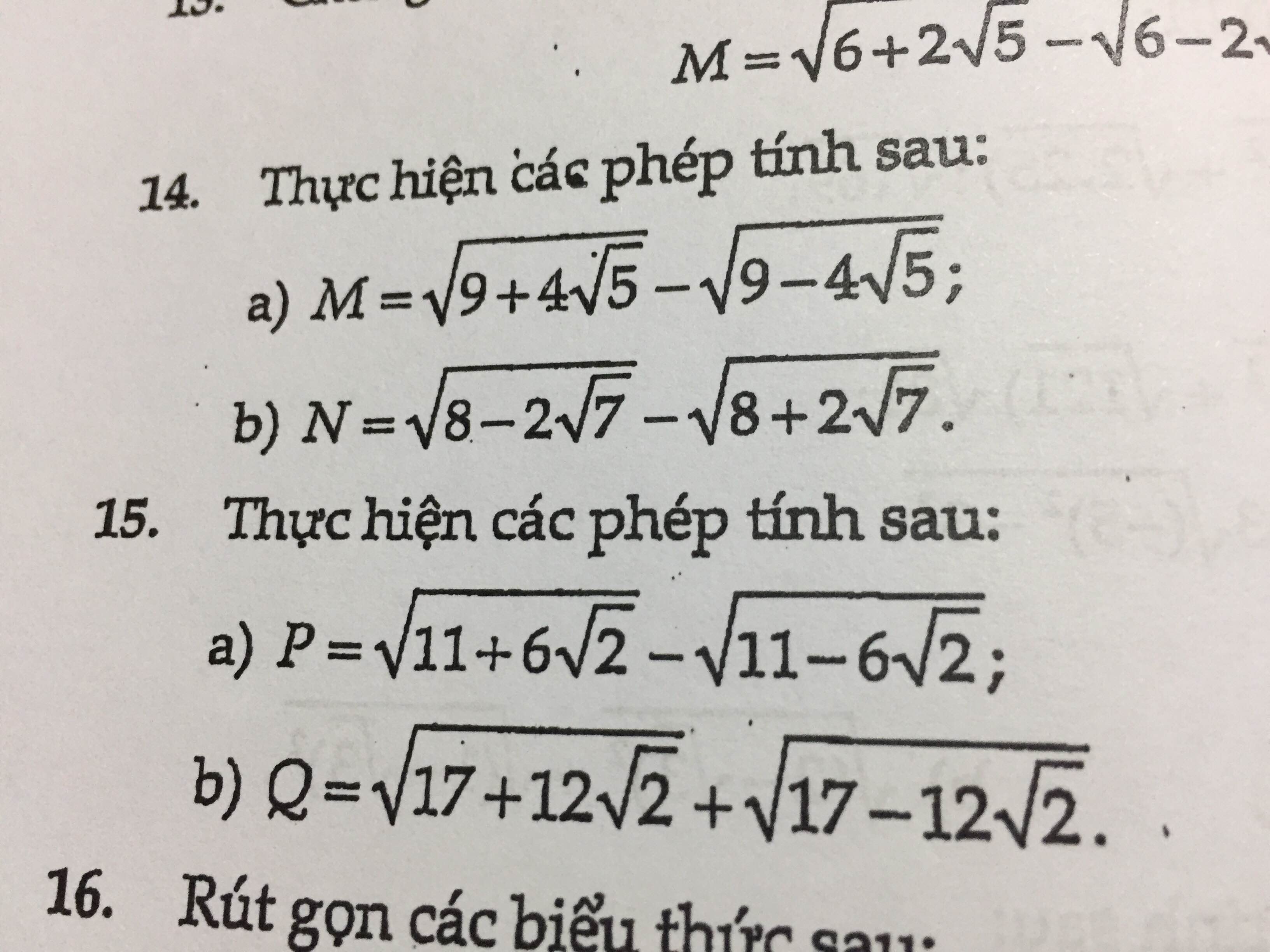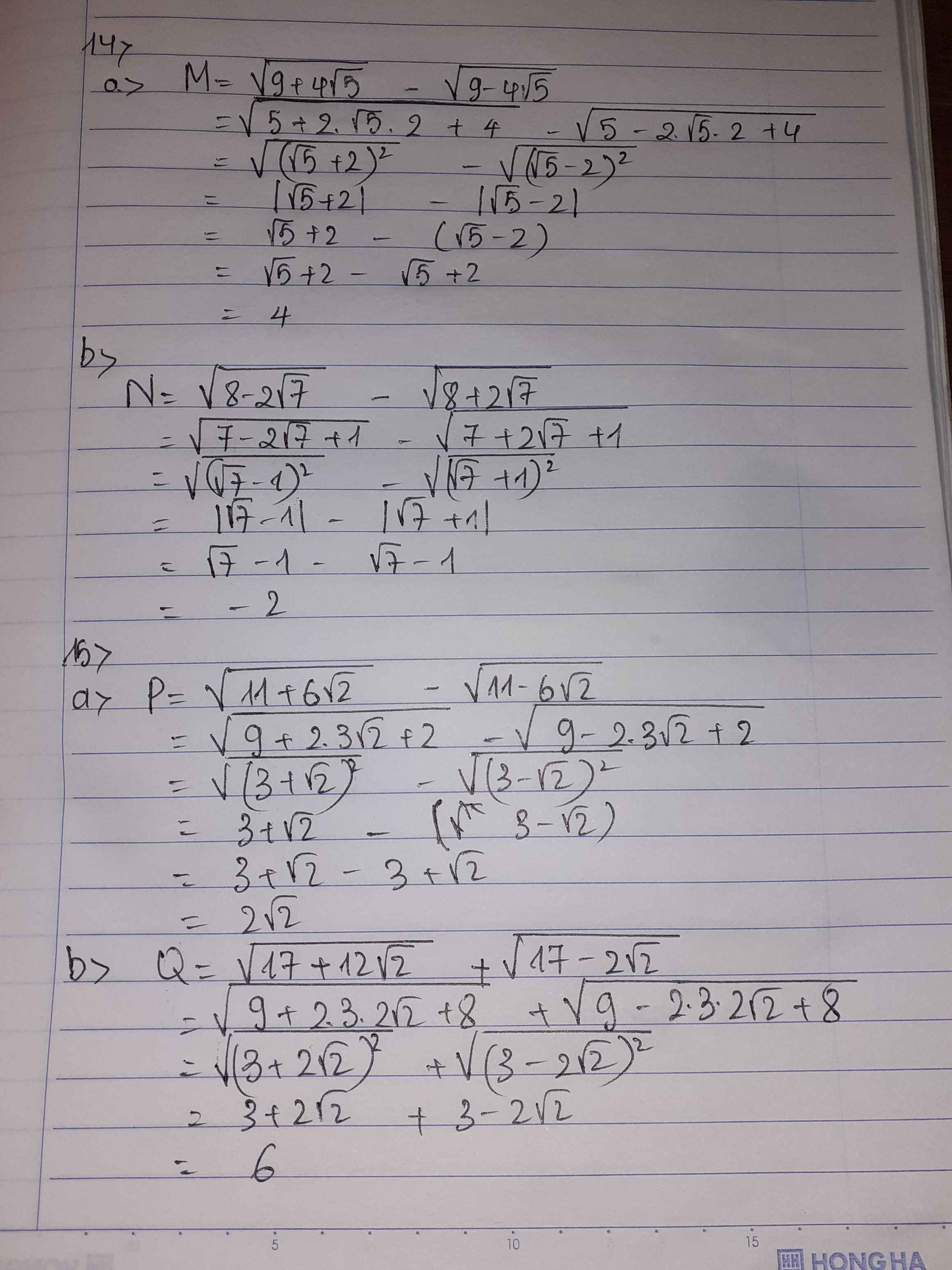14a) \(M=\sqrt{9+4\sqrt{5}}-\sqrt{9-4\sqrt{5}}\)
\(=\sqrt{\left(\sqrt{5}\right)^2+2.\sqrt{2}.2+2^2}-\sqrt{\left(\sqrt{5}\right)^2-2.\sqrt{2}.2+2^2}\)
\(=\sqrt{\left(\sqrt{5}+2\right)^2}-\sqrt{\left(\sqrt{5}-2\right)^2}=\left|\sqrt{5}+2\right|-\left|\sqrt{5}-2\right|\)
\(=\sqrt{5}+2-\sqrt{5}+2=4\)
b) \(N=\sqrt{8-2\sqrt{7}}-\sqrt{8+2\sqrt{7}}\)
\(=\sqrt{\left(\sqrt{7}\right)^2-2.\sqrt{7}.1+1^2}-\sqrt{\left(\sqrt{7}\right)^2+2.\sqrt{7}.1+1^2}\)
\(=\sqrt{\left(\sqrt{7}-1\right)^2}-\sqrt{\left(\sqrt{7}+1\right)^2}=\left|\sqrt{7}-1\right|-\left|\sqrt{7}+1\right|\)
\(=\sqrt{7}-1-\sqrt{7}-1=-2\)
15a) \(P=\sqrt{11+6\sqrt{2}}-\sqrt{11-6\sqrt{2}}\)
\(=\sqrt{3^2+2.3.\sqrt{2}+\left(\sqrt{2}\right)^2}-\sqrt{3^2-2.3.\sqrt{2}+\left(\sqrt{2}\right)^2}\)
\(=\sqrt{\left(3+\sqrt{2}\right)^2}-\sqrt{\left(3-\sqrt{2}\right)^2}=\left|3+\sqrt{2}\right|-\left|3-\sqrt{2}\right|\)
\(=3+\sqrt{2}-3+\sqrt{2}=2\sqrt{2}\)
b) \(Q=\sqrt{17+12\sqrt{2}}+\sqrt{17-12\sqrt{2}}\)
\(=\sqrt{3^2+2.3.2\sqrt{2}+\left(2\sqrt{2}\right)^2}+\sqrt{3^2-2.3.2\sqrt{2}+\left(2\sqrt{2}\right)^2}\)
\(=\sqrt{\left(3+2\sqrt{2}\right)^2}+\sqrt{\left(3-2\sqrt{2}\right)^2}=\left|3+2\sqrt{2}\right|+\left|3-2\sqrt{2}\right|\)
\(=3+2\sqrt{2}+3-2\sqrt{2}=6\)
Bài 14:
a) Ta có: \(M=\sqrt{9+4\sqrt{5}}-\sqrt{9-4\sqrt{5}}\)
\(=\sqrt{5}+2-\sqrt{5}+2\)
=4
b) Ta có: \(N=\sqrt{8-2\sqrt{7}}-\sqrt{8+2\sqrt{7}}\)
\(=\sqrt{7}-1-\sqrt{7}-1\)
=-2
Bài 15:
a) Ta có: \(P=\sqrt{11+6\sqrt{2}}-\sqrt{11-6\sqrt{2}}\)
\(=3+\sqrt{2}-3+\sqrt{2}\)
\(=2\sqrt{2}\)
b) Ta có: \(Q=\sqrt{17+12\sqrt{2}}+\sqrt{17-12\sqrt{2}}\)
\(=3+2\sqrt{2}+3-2\sqrt{2}\)
=6