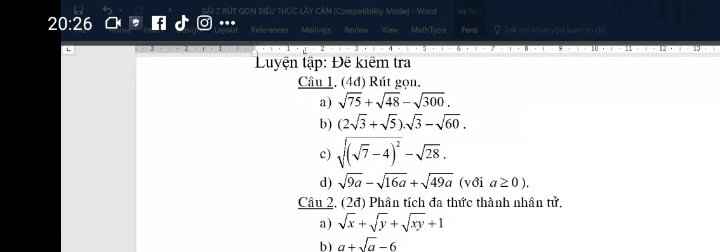
!
Bài 3:
\(A=\sqrt{1-6x+9x^2}+\sqrt{9x^2-12x+4}\)
\(A=\sqrt{9x^2-3x-3x+1}+\sqrt{9x^2-6x-6x+4}\)
\(A=\sqrt{\left(3x-1\right)^2}+\sqrt{\left(3x-2\right)^2}\)
\(A=\left|3x-1\right|+\left|3x-2\right|\)
\(A=\left|3x-1\right|+\left|2-3x\right|\)
Áp dụng bất đẳng thức \(\left|A\right|+\left|B\right|\ge\left|A+B\right|\) ta có:
\(\left|3x-1\right|+\left|2-3x\right|\ge\left|3x-1+2-3x\right|\)
\(\Rightarrow\left|3x-1\right|+\left|2-3x\right|\ge\left|1\right|=1\)
Dấu "=" sảy ra khi và chỉ khi:
\(\left\{{}\begin{matrix}3x-1\ge0\\2-3x\ge0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}3x\ge1\\3x\le2\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x\ge\dfrac{1}{3}\\x\le\dfrac{2}{3}\end{matrix}\right.\)
\(\Rightarrow\dfrac{1}{3}\le x\le\dfrac{2}{3}\)
Vậy............
Chúc bạn học tốt!!!
1 A\(=\sqrt{4\cdot5}-\sqrt{9\cdot5}+3\sqrt{9\cdot2}+\sqrt{36\cdot2}\)
\(=2\sqrt{5}-3\sqrt{5}+9\sqrt{2}+6\sqrt{2}\)
\(=\left(2\sqrt{5}-3\sqrt{5}\right)+\left(9\sqrt{2}+6\sqrt{2}\right)\)
\(=-\sqrt{5}+15\sqrt{2}\)
3 2 ve tren la hang dang thuc dang nho nen chuyen sang hdt
A=\(\sqrt{1-2\cdot3x+9x^2}+\sqrt{9x^2-2\cdot3x\cdot2+4}\)
\(=\sqrt{\left(1-3x\right)^2}+\sqrt{\left(3x-2\right)^2}\ge0\)
vay GTNN
2 GTNN cua \(x-\sqrt{x}+1\)
\(=x-2\sqrt{x}\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}\)
\(=\left(x-2\sqrt{x}\dfrac{1}{2}+\dfrac{1}{4}\right)+\dfrac{3}{4}\)
\(=\left(x-\dfrac{1}{4}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\)
vay GTNN la \(\dfrac{3}{4}\Rightarrow GTLN:\dfrac{1}{\dfrac{3}{4}}=\dfrac{4}{3}\)
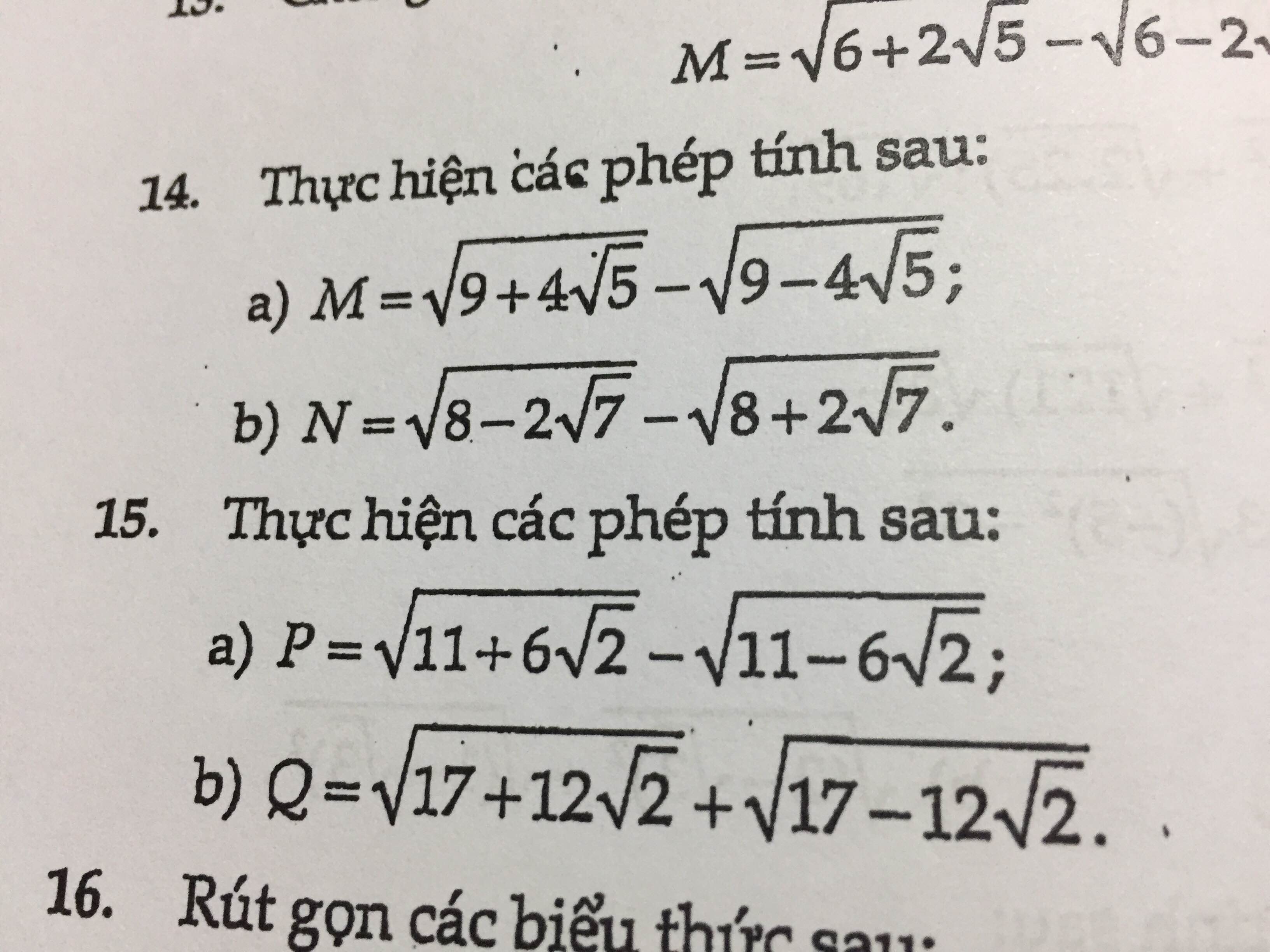
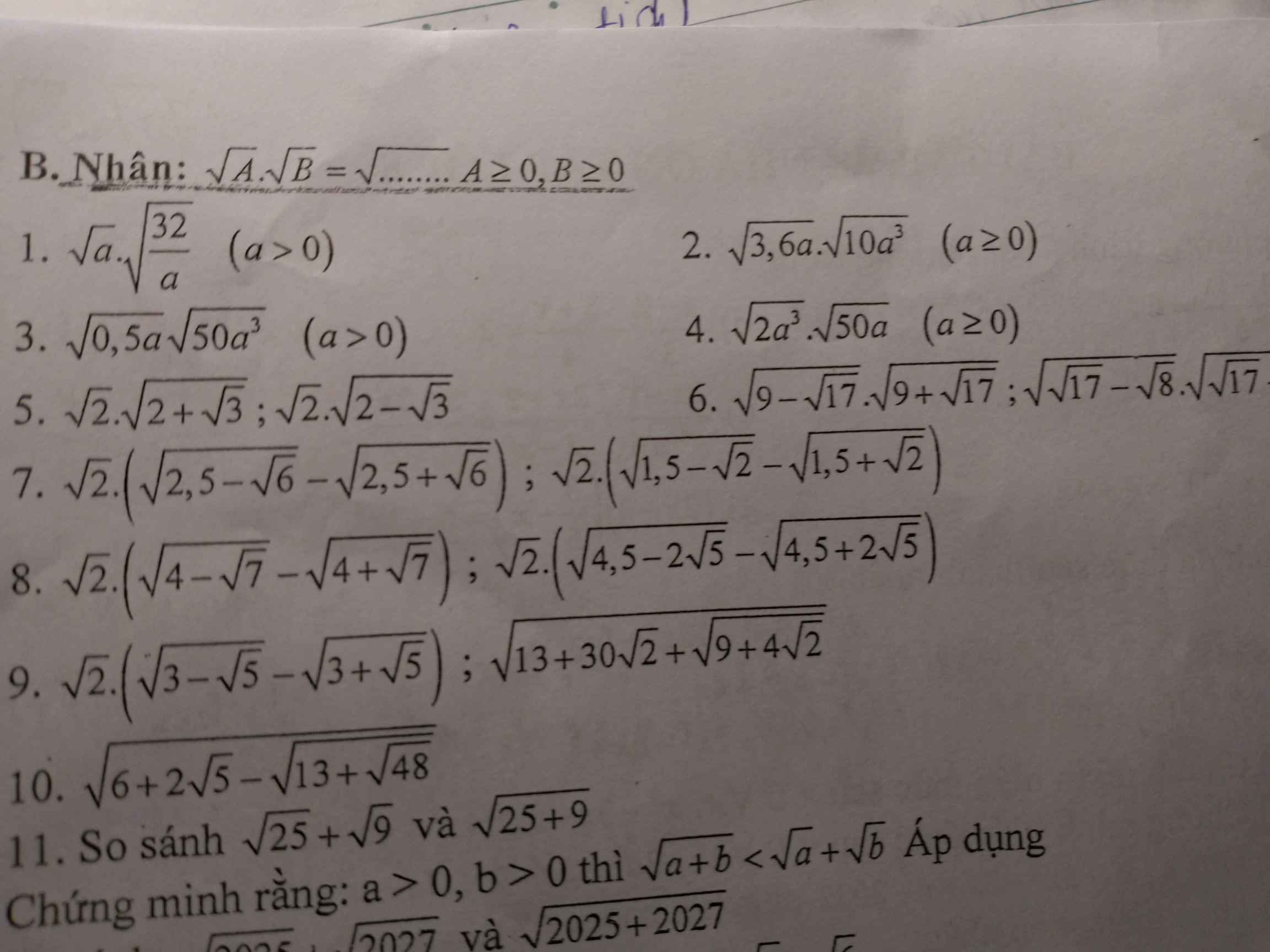
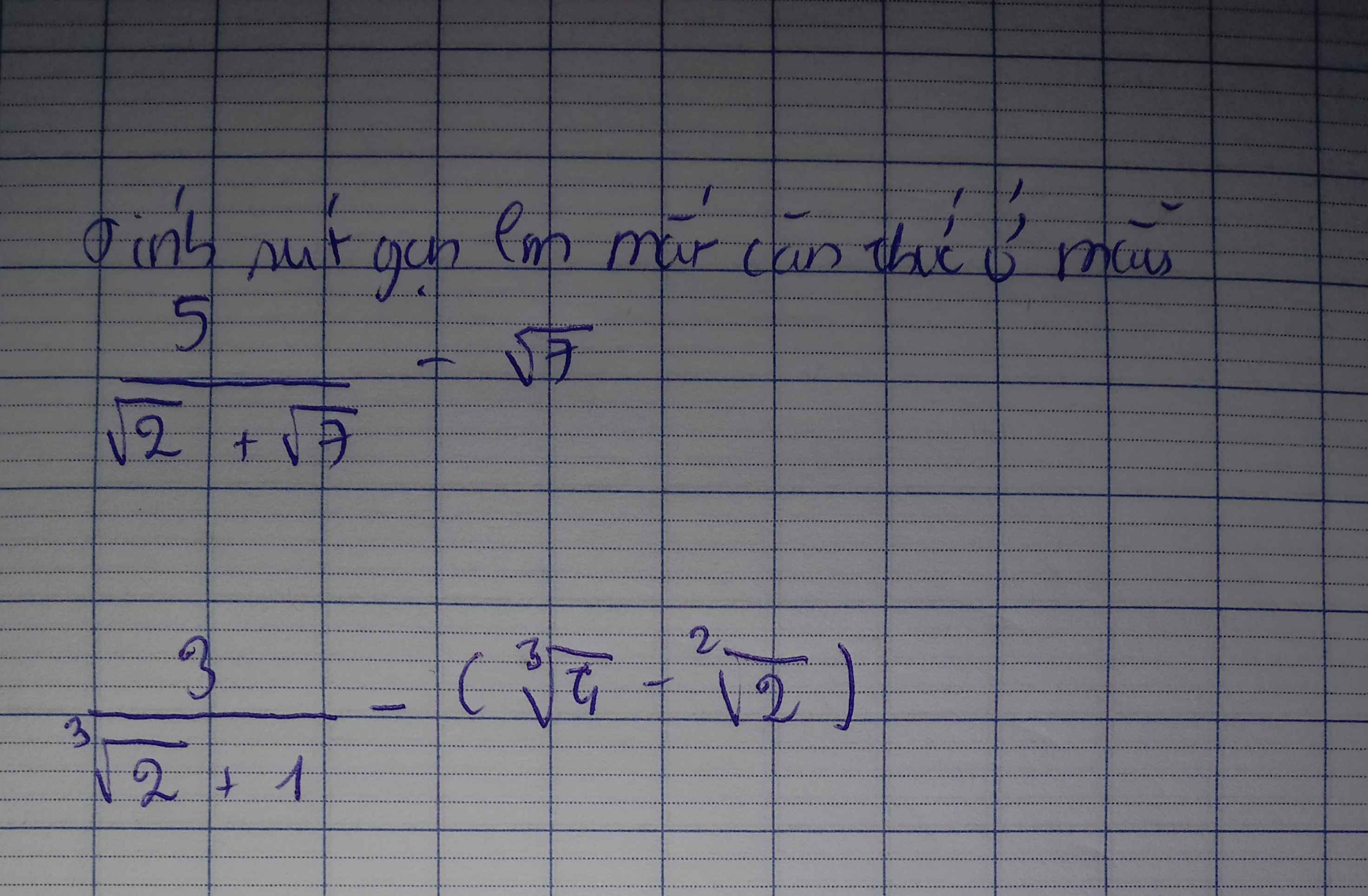
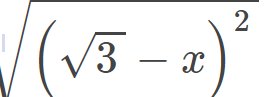
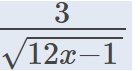GIÚP MÌNH VỚI Ạ MÌNH CẦN GẤP Ạ
