b) \(x^2+xy=3x+y+1< =>x\left(x-1\right)+y\left(x-1\right)-2\left(x-1\right)=3\)
\(< =>=>\left(x-1\right)\left(x+y-2\right)=3\)
\(\left[{}\begin{matrix}\left\{{}\begin{matrix}x-1=3\\x+y-2=1\end{matrix}\right.< =>\left\{{}\begin{matrix}x=4\\y=-1\end{matrix}\right.\\\left\{{}\begin{matrix}x-1=-3\\x+y-2=-1\end{matrix}\right.< =>\left\{{}\begin{matrix}x=-2\\y=3\end{matrix}\right.\\\left\{{}\begin{matrix}x-1=1\\x+y-2=3\end{matrix}\right.< =>\left\{{}\begin{matrix}x=2\\y=3\end{matrix}\right.\\\left\{{}\begin{matrix}x-1=-1\\x+y-2=-3\end{matrix}\right.< =>\left\{{}\begin{matrix}x=0\\y=-1\end{matrix}\right.\end{matrix}\right.\)
c) \(xy-y-x\sqrt{y-1}-y\sqrt{x-3}=0\)
\(2xy-2y-2x\sqrt{y-1}-2y\sqrt{x-3}=0\)
\(< =>x\left(y-1+2\sqrt{y-1}+1\right)+y\left(x-3+2\sqrt{x-3}+1\right)=0\)
\(< =>x\left(\sqrt{y-1}-1\right)^2+y\left(\sqrt{x-3}-1\right)^2=0\)
\(dk:\left\{{}\begin{matrix}x\ge3\\y\ge1\end{matrix}\right.\)
\(< =>\left\{{}\begin{matrix}\sqrt{y-1}-1=0\\\sqrt{x-3}-1=0\end{matrix}\right.< =>\left\{{}\begin{matrix}y=2\\x=4\end{matrix}\right.\)
tu thay M vao tinh not nhe






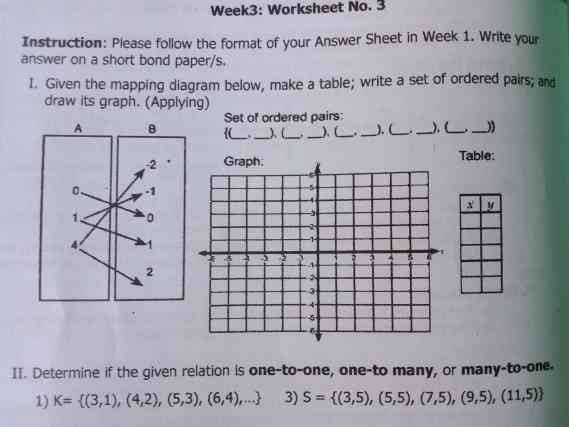




 giúp mk câu b vs
giúp mk câu b vs





