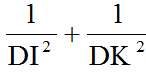Ta có: \(\dfrac{AB}{AC}=\dfrac{2}{3}\). Gọi \(AB=2x\left(cm\right),AC=3x\left(cm\right)\)
Áp dụng định lý Pytago trong tam giác vuông ABC:
\(BC^2=AB^2+AC^2=4x^2+9x^2=13x^2\)
\(\Rightarrow BC=\sqrt{13}x\)
Xét tam giác ABC vuông tại A có đường cao AH:
\(AH.BC=AB.AC\)(hệ thức lượng trong tam giác vuông)
\(\Rightarrow6\sqrt{13}x=6x^2\)
\(\Rightarrow x^2-\sqrt{13}x=0\)
Vì x > 0
\(\Rightarrow x=\sqrt{13}\left(cm\right)\)
\(\Rightarrow\left\{{}\begin{matrix}AB=2x=2\sqrt{13}\left(cm\right)\\AC=3x=3\sqrt{13}\left(cm\right)\\BC=\sqrt{13}x=13\left(cm\right)\end{matrix}\right.\)
Ta có: \(\dfrac{AB}{AC}=\dfrac{2}{3}\)
nên \(\dfrac{HB}{HC}=\dfrac{4}{9}\)
\(\Leftrightarrow HB=\dfrac{4}{9}HC\)
Ta có: \(AH^2=HB\cdot HC\)
\(\Leftrightarrow HC^2\cdot\dfrac{4}{9}=36\)
\(\Leftrightarrow HC^2=16\)
\(\Leftrightarrow HC=4\left(cm\right)\)
\(\Leftrightarrow HB=9\left(cm\right)\)
Ta có: BH+HC=BC
nên BC=4+9=13(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=2\sqrt{13}\left(cm\right)\\AC=3\sqrt{13}\left(cm\right)\end{matrix}\right.\)
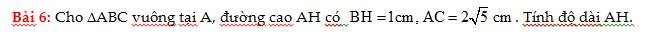giúp mình bài này với ạ
