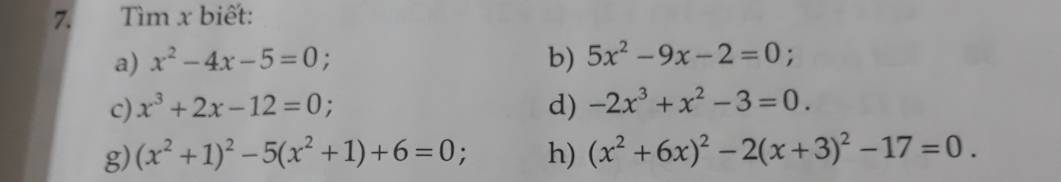`a, x^2-4x-5=0`
`<=>x^2+x-5x-5=0`
`<=> (x^2+x)-(5x+5)=0`
`<=> x(x+1)-5(x+1)=0`
`<=>(x+1)(x-5)=0`
\(\Leftrightarrow\left[{}\begin{matrix}x+1=0\\x-5=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\x=5\end{matrix}\right.\)
`b, 5x^2-9x-2=0`
`<=> 5x^2+x-10x-2=0`
`<=> (5x^2+x)-(10x+2)=0`
`<=> x(5x+1)-2(5x+1)=0`
`<=>(5x+1)(x-2)=0`
\(\Leftrightarrow\left[{}\begin{matrix}5x+1=0\\x-2=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}5x=-1\\x=2\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{5}\\x=2\end{matrix}\right.\)
`c, x^3+2x-12=0`
`<=> x^3+2x-8-4=0`
`<=> (x^3-8)+(2x-4)=0`
`<=> (x-2)(x^2 + 2x+4) + 2(x-2)=0`
`<=>(x-2)(x^2+2x+4+2)=0`
`<=>(x-2)(x^2+2x+6)=0`
`<=>x-2=0`
`<=>x=2`
`d, -2x^3 +x^2-3=0`
`<=> -(2x^3-x^2+3)=0`
`<=> -(2x^3 -3x^2 +3x+2x^2 -3x+3)=0`
`<=>-[(2x^3 -3x^2 +3x) +(2x^2-3x+3)]=0`
`<=> - [x(2x^3 -3x^2 +3x) +(2x^2-3x+3)]=0`
`<=> -(2x^3-3x^2+3x)(x+1)=0`
`<=>x+1=0`
`<=>x=-1`
\(a,x^2-4x-5=0\\ \Leftrightarrow x^2+x-5x-5=0\\ \Leftrightarrow x\left(x+1\right)-5\left(x+1\right)=0\\ \Leftrightarrow\left(x-5\right)\left(x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-5=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\x=-1\end{matrix}\right.\\ b,5x^2-9x-2=0\\ \Leftrightarrow5x^2-10x+x-2=0\\ \Leftrightarrow5x\left(x-2\right)+\left(x-2\right)=0\\ \Leftrightarrow\left(5x+1\right)\left(x-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}5x+1=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{5}\\x=2\end{matrix}\right.\)
c) x³ + 2x - 12 = 0
x³ - 2x² + 2x² - 4x + 6x - 12 = 0
(x³ - 2x²) + (2x² - 4x) + (6x - 12) = 0
x²(x - 2) + 2x(x - 2) + 6(x - 2) = 0
(x - 2)(x² + 2x + 6) = 0
⇒ x - 2 = 0 (vì x² + 2x + 6 > 0 với mọi x ∈ R)
x = 0 + 2
x = 2
Vậy x = 2
d) -2x³ + x² - 3 = 0
-2x³ - 2x² + 3x² - 3 = 0
(-2x³ - 2x²) + (3x² - 3) = 0
-2x²(x + 1) + 3(x² - 1) = 0
-2x²(x + 1) + 3(x + 1)(x - 1) = 0
(x + 1)(-2x² + 3x - 3) = 0
⇒ x + 1 = 0 (vì -2x² + 3x - 3 < 0 với mọi x ∈ R)
x = -1
Vậy x = -1
g) (x² + 1)² - 5(x² + 1) + 6 = 0
Đặt m = x² + 1 (m > 0), ta có:
m² - 5m + 6 = 0
m² - 2m - 3m + 6 = 0
(m² - 2m) - (3m - 6) = 0
m(m - 2) - 3(m - 2) = 0
(m - 2)(m - 3) = 0
⇒ m - 2 = 0 hoặc m - 3 = 0
*) m - 2 = 0
m = 2 (nhận)
*) m - 3 = 0
m = 3 (nhận)
* Với m = 2
⇒ x² + 1 = 2
⇒ x² = 2 - 1
⇒ x² = 1
⇒ x = 1 hoặc x = -1
* Với m = 3
⇒ x² + 1 = 3
⇒ x² = 3 - 1
⇒ x² = 2
⇒ x = -√2 hoặc x = √2
Vậy x = -√2; x = -1; x = 1; x = √2
h) (x² + 6x)² - 2(x + 3)² - 17 = 0
x⁴ + 12x³ + 36x² - 2x² - 12x - 18 - 17 = 0
x⁴ + 12x³ + 34x² - 12x - 35 = 0
x⁴ + x³ + 11x³ + 11x² + 23x² + 23x - 35x - 35 = 0
(x⁴ + x³) + (11x³ + 11x²) + (23x² + 23x) - (35x + 35) = 0
x³(x + 1) + 11x²(x + 1) + 23x(x + 1) - 35(x + 1) = 0
(x + 1)(x³ + 11x² + 23x - 35) = 0
(x + 1)(x³ - x² + 12x² - 12x + 35x - 35) = 0
(x + 1)[(x³ - x²) + (12x² - 12x) + (35x - 35)] = 0
(x + 1)[x²(x - 1) + 12x(x - 1) + 35(x - 1)] = 0
(x + 1)(x - 1)(x² + 12x + 35) = 0
(x + 1)(x - 1)(x² + 5x + 7x + 35) = 0
(x + 1)(x - 1)[(x² + 5x) + (7x + 35)] = 0
(x + 1)(x - 1)[x(x + 5) + 7(x + 5)] = 0
(x + 1)(x - 1)(x + 5)(x + 7) = 0
x + 1 = 0 hoặc x - 1 = 0 hoặc x + 5 = 0 hoặc x + 7 = 0
*) x + 1 = 0
x = -1
*) x - 1 = 0
x = 1
*) x + 5 = 0
x = -5
*) x + 7 = 0
x = -7
Vậy x = -7; x = -5; x = -1; x = 1