\(a,\dfrac{13z}{63x^2y^3}=\dfrac{65z^3}{315x^2y^3z^2};\dfrac{-y}{15xz^2}=\dfrac{-21xy^4}{315x^2y^3z^2};\dfrac{2x}{9y^2z}=\dfrac{70x^3yz}{315x^2y^3z}\\ b,\dfrac{x}{x-y}=\dfrac{-x\left(y-x\right)^2}{\left(y-x\right)^3};\dfrac{y}{\left(x-y\right)^2}=\dfrac{y}{\left(y-x\right)^2}=\dfrac{y}{\left(y-x\right)^3}\\ c,\dfrac{1}{2x+4}=\dfrac{x-2}{2\left(x+2\right)\left(x-2\right)};\dfrac{x}{2x-4}=\dfrac{x\left(x+2\right)}{2\left(x-2\right)\left(x+2\right)};\dfrac{3}{4-x^2}=-\dfrac{6}{2\left(x-2\right)\left(x+2\right)}\)
Bài 4: Quy đồng mẫu thức nhiều phân thức
Đúng 3
Bình luận (0)
Các câu hỏi tương tự
Giải giúp em bài 4,5 vs ạ . Em cảm ơn .
Giúp e vs ạ, xin mng hãy giúp e, e nhiều bài tập quá
G iúp mình vs càng nhanh càng tốt ạ
iúp mình vs càng nhanh càng tốt ạ
Em Cần Gấp Ạ Hãy Giúp Em Với Ạ
Quy đồng mẫu 2 phân thức sau:
Mn ơi giúp em với ạ, 10h là em nộp bài rồi ạ!
giúp em bài 1 với ạ, em cần gấp
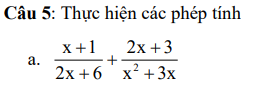
giúp em gấp ạ
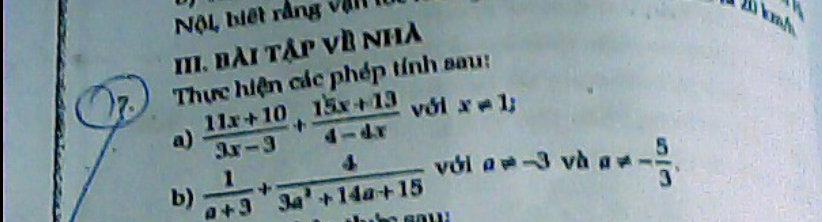
Mn giúp em với ạ

mọi người giúp em với ạ T.T














