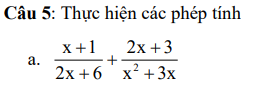\(=\dfrac{x+1}{2\left(x+3\right)}+\dfrac{2x+3}{x\left(x+3\right)}=\dfrac{x\left(x+1\right)+\left[2\left(2x+3\right)\right]}{2x\left(x+3\right)}=\dfrac{x^2+x+4x+6}{2x\left(x+3\right)}=\dfrac{x^2+5x+6}{2x\left(x+3\right)}=\dfrac{\left(x+2\right)\left(x+3\right)}{2x\left(x+3\right)}=\dfrac{x+2}{2x}\)
\(\dfrac{x+1}{2x+6}\) + \(\dfrac{2x+3}{x^2+3x}\) = \(\dfrac{x+1}{2\left(x+3\right)}\) + \(\dfrac{2x+3}{x\left(x+3\right)}\)
MTC: 2x ( x + 3 )
=> \(\dfrac{x\left(x+1\right)}{2x\left(x+3\right)}\) + \(\dfrac{2\left(2x+3\right)}{2x\left(x+3\right)}\) = \(\dfrac{x^2+x+4x+6}{2x\left(x+3\right)}\) = \(\dfrac{x^2+5x+6}{2x\left(x+3\right)}\) = \(\dfrac{\left(x+2\right)\left(x+3\right)}{2x\left(x+3\right)}\) = \(\dfrac{x+2}{2x}\)