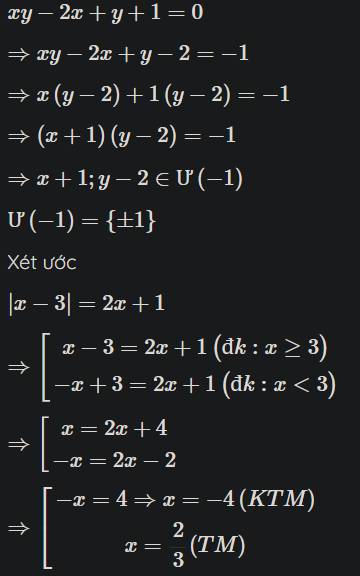\(xy-2x+y-2+3=0\\ \Leftrightarrow x\left(y-2\right)+\left(y-2\right)=-3\\\Leftrightarrow \left(x+1\right)\left(y-2\right)=-3\)
\(TH1:\left\{{}\begin{matrix}x+1=1\\y-2=-3\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=0\\y=-1\end{matrix}\right.\\ TH2:\left\{{}\begin{matrix}x+1=-3\\y-2=1\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=-4\\y=3\end{matrix}\right.\\ TH3:\left\{{}\begin{matrix}x+1=-1\\y-2=3\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=-2\\y=5\end{matrix}\right.\\ TH4:\left\{{}\begin{matrix}x+1=3\\y-2=-1\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)
Vậy \(\left(0;-1\right);\left(-4;3\right);\left(-2;5\right);\left(2;1\right)\)