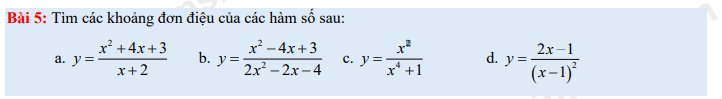tách từng bài ra nha bn, dài quá ko ai làm đâu ạ
5.
\(y'=\dfrac{m^2-9}{\left(x+m\right)^2}\)
Hàm nghịch biến trên các khoảng xác định khi \(m^2-9< 0\)
\(\Rightarrow-3< m< 3\)
\(\Rightarrow S=\left\{-2;-1;0;1;2\right\}\)
6.
\(y'=\dfrac{-m^2+4}{\left(x-m\right)^2}\)
Hàm đồng biến trên khoảng đã cho khi:
\(\left\{{}\begin{matrix}-m^2+4>0\\m\le-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-2< m< 2\\m\le-1\end{matrix}\right.\)
\(\Rightarrow-2< m\le-1\)
7.
\(y'=\dfrac{-m-8}{\left(2x-m\right)^2}\)
Hàm nghịch biến trên khoảng đã cho khi:
\(\left\{{}\begin{matrix}-m-8< 0\\\left[{}\begin{matrix}\dfrac{m}{2}\ge4\\\dfrac{m}{2}\le-3\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>-8\\\left[{}\begin{matrix}m\ge8\\m\le-6\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow\) Có 2 giá trị nguyên âm của m thỏa mãn\(\left(m=-7;-6\right)\)
8.
Từ đồ thị ta thấy \(f'\left(x\right)\le0\) khi \(\left[{}\begin{matrix}x\le-1\\1\le x\le4\end{matrix}\right.\)
\(y'=-f'\left(2-x\right)\)
\(\Rightarrow y=f\left(2-x\right)\) đồng biến khi \(-f'\left(2-x\right)\ge0\)
\(\Rightarrow f'\left(2-x\right)\le0\)
\(\Rightarrow\left[{}\begin{matrix}2-x\le-1\\1\le2-x\le4\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x\ge3\\-2\le x\le1\end{matrix}\right.\)
B đúng
9.
\(y=3f\left(x+2\right)-x^3+3x\)
\(\Rightarrow y'=3f'\left(x+2\right)-3x^2+3\)
\(y'\ge0\Rightarrow f'\left(x+2\right)\ge x^2-1\)
\(\Rightarrow B\) đúng (do trên \(x\in\left(-1;0\right)\Rightarrow x^2-1\le0\), đồng thời \(x+2\in\left(1;2\right)\Rightarrow f'\left(x+2\right)\ge0\)
\(\Rightarrow f'\left(x+2\right)\ge x^2-1\)
10.
\(g'\left(x\right)=-2f'\left(1-2x\right)+2x-1\)
\(g'\left(x\right)\le0\Rightarrow f'\left(1-2x\right)\ge-\dfrac{1}{2}\left(1-2x\right)\)
Vẽ lên cùng hệ trục của \(f'\left(x\right)\) đường thẳng \(y'=-\dfrac{1}{2}x\), ta thấy \(f'\left(1-2x\right)\ge-\dfrac{1}{2}\left(1-2x\right)\) khi:
\(\left[{}\begin{matrix}-2\le1-2x\le0\\1-2x\ge4\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}\dfrac{1}{2}\le x\le\dfrac{3}{2}\\x\le-\dfrac{3}{2}\end{matrix}\right.\)
A đúng
11.D
12D
13 Từ BBT ta thấy:
Hàm đồng biến trên các khoảng \(\left(-\infty;-\dfrac{1}{2}\right)\) và \(\left(-\dfrac{1}{2};3\right)\) (cũng như các tập con của chúng)
Hàm nghịch biến trên \(\left(3;+\infty\right)\) (cũng như các tập con của nó)
C đúng
14.
Hàm nghịch biến trên các khoảng \(\left(-2;0\right)\) và \(\left(2;+\infty\right)\)
15.
\(y'=\dfrac{3}{\left(x+1\right)^2}>0;\forall x\ne-1\)
\(\Rightarrow\) Hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(-1;+\infty\right)\)
D đúng
16.
Hàm trùng phương (câu A) luôn có khoảng đồng biến và nghịch biến (nên ko bao giờ đồng biến hoặc nghịch biến trên R)
Hàm bậc nhất trên bậc nhất (câu B) luôn có điểm gián đoạn (mẫu thức ko xác định) nên ko bao giờ đồng biến/nghịch biến trên toàn miền R
Với câu C ta có \(y'=3x^2+3>0;\forall x\Rightarrow\) đồng biến trên R (đúng)
17.
\(y'=3x^2-6x=0\Rightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
Hàm đồng biến trên các khoảng \(\left(-\infty;0\right)\) và\(\left(2;+\infty\right)\)
Hàm nghịch biến trên \(\left(0;2\right)\)
B đúng
18.
Câu này rất có thể đề bài in sai, đề đúng là \(y=x^3-3mx^2+3\left(2m-1\right)x+1\)
\(y'=3x^2-6mx+3\left(2m-1\right)\)
Hàm đồng biến trên R khi \(\Delta'=9m^2-9\left(2m-1\right)\le0\)
\(\Leftrightarrow9\left(m-1\right)^2\le0\)
\(\Rightarrow m=1\)
19.
\(y'=\dfrac{m-1}{\left(x+1\right)^2}\)
Hàm nghịch biến trên các khoảng xác định khi: \(m-1< 0\)
\(\Rightarrow m< 1\)
(Lưu ý: hàm bậc nhất trên bậc nhất thì ko có dấu "=" khi so sánh y' với 0)
20.
\(y'=\dfrac{m-4}{\left(x+m\right)^2}\)
Hàm đồng biến trên khoảng đã cho khi:
\(\left\{{}\begin{matrix}m-4>0\\-m\ge-7\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>4\\m\le7\end{matrix}\right.\)
\(\Rightarrow4< m\le7\) (B)
21.
\(y'=3x^2-6mx\)
Hàm nghịch biến trên khoảng đã cho khi:
\(3x^2-6mx\le0\) ; \(\forall x\in\left(0;1\right)\)
\(\Leftrightarrow2mx\ge x^2\)
\(\Rightarrow m\ge\dfrac{x}{2}\)
\(\Rightarrow m\ge\max\limits_{\left(0;1\right)}\dfrac{x}{2}=\dfrac{1}{2}\)
22.
\(f'\left(x\right)=x\left(x-2\right)^3=0\Rightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
\(\Rightarrow\)Hàm đồng biến trên các khoảng \(\left(-\infty;0\right)\) và \(\left(2;+\infty\right)\) (cũng như các tập con của chúng)
Hàm nghịch biến trên \(\left(0;2\right)\) (cũng như các tập con của nó)
\(\Rightarrow C\) đúng do \(\left(0;1\right)\subset\left(0;2\right)\)
23.
\(y'=x^2\ge0;\forall x\in R\)
\(\Rightarrow\) Hàm đồng biến trên R












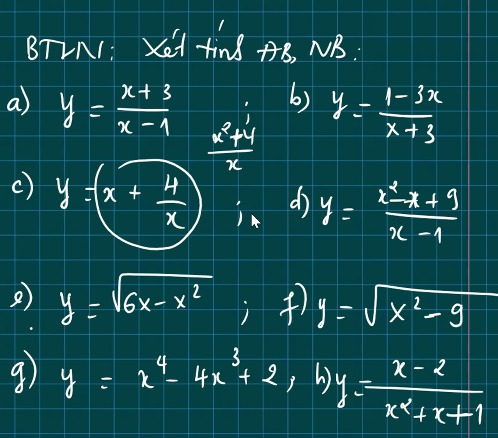 Cho em xin lời giải chi tiết với ạ
Cho em xin lời giải chi tiết với ạ