\(a,PT\Leftrightarrow\left[{}\begin{matrix}2x-1=x+3\left(x\ge\dfrac{1}{2}\right)\\1-2x=x+3\left(x< \dfrac{1}{2}\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\left(tm\right)\\x=-\dfrac{2}{3}\left(tm\right)\end{matrix}\right.\\ b,PT\Leftrightarrow\left[{}\begin{matrix}\left(x+1\right)\left(2x-5\right)=5\left(x+1\right)\left(x\le-1;x\ge\dfrac{5}{2}\right)\\\left(x+1\right)\left(2x-5\right)=-5\left(x+1\right)\left(-1< x< \dfrac{5}{2}\right)\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}\left(x+1\right)\left(2x-10\right)=0\\2x\left(x+1\right)=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=5\\x=0\end{matrix}\right.\)
\(c,\Leftrightarrow\left[{}\begin{matrix}x-2=3x^2-x-2\left(x\ge2\right)\\2-x=3x^2-x-2\left(x< 2\right)\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x\left(3x-2\right)=0\left(x\ge2\right)\\3x^2=4\left(x< 2\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2}{\sqrt{3}}\\x=-\dfrac{2}{\sqrt{3}}\end{matrix}\right.\)









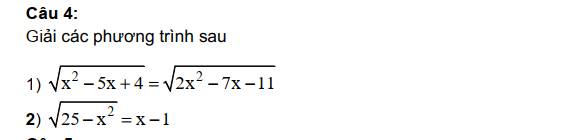




 Giúp em vs ạ
Giúp em vs ạ
 giúp em với ạ
giúp em với ạ

