\(\Rightarrow x^2+y^2⋮7\) mà \(7\equiv3\left(mod4\right)\)
\(\Rightarrow x^2⋮7,y^2⋮7\)
Đặt \(x=7x_1;y=7y_1\)
\(49x_1^2+49y_1^2=7z^2\)
Tới đây tự làm tiếp nhé
Giải phương trình nghiệm nguyên \(x^2+y^2+2x+2y=x^2y^2-1\)
Tìm nghiệm nguyên không âm thỏa mãn phương trình: x^2=y^2 + căn y+1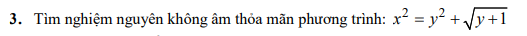
Tìm nghiệm nguyên của phương trình: \(x^2-25=y.\left(y+6\right)\)
1) Chứng minh rằng: \(x^3-7y=51\) không có nghiệm nguyên
2) Tìm nghiệm nguyên của phương trình \(x^2-5y^2=27\)
3) Tìm nghiệm nguyên dương
a) \(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}=1\)
b)\(\dfrac{1}{x}+\dfrac{1}{y}=z\)
Cho hệ phương trình: 2X +Y = 3m-2 ( m là tham số ) X - Y = 5 a) Giải hệ phương trình khi m = - 4 ; b) Tìm m để hệ phương trình có nghiệm (x; y) thỏa mãn: x + y = 13.
Tìm nghiệm nguyên dương của phương trình : \(\sqrt{x+2\sqrt{3}}=\sqrt{y}+\sqrt{z}\)
Giải phương trình nghiệm nguyên \(3x^2+5xy-8x-2y^2-9y-4=0\)
Giải phương trình nghiệm nguyên: 2x^2-xy+7y^3=4880
cho phương trình x^2-6x+m-2=0
a,giải phương trình khi m=2
b,tìm m để phương trình có nghiệm kép,tìm nghiệm đó
