Áp dụng hệ thức lượng:
\(AB^2=BH.BC\Leftrightarrow20^2=BH\left(BH+9\right)\)
\(\Leftrightarrow BH^2+9BH-400=0\Rightarrow\left[{}\begin{matrix}BH=-25\left(loại\right)\\BH=16\end{matrix}\right.\)
Áp dụng hệ thức lượng:
\(AH^2=BH.CH\Rightarrow AH=\sqrt{BH.CH}=\sqrt{16.9}=12\left(cm\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AB^2=HB\cdot BC\)
\(\Leftrightarrow HB\left(HB+9\right)=400\)
\(\Leftrightarrow HB^2+25HB-16HB-400=0\)
\(\Leftrightarrow HB=16\)
Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:
\(AB^2=AH^2+HB^2\)
\(\Leftrightarrow AH^2=20^2-16^2=144\)
hay AH=12(cm)

 giải giúp
giải giúp



 giải giúp
giải giúp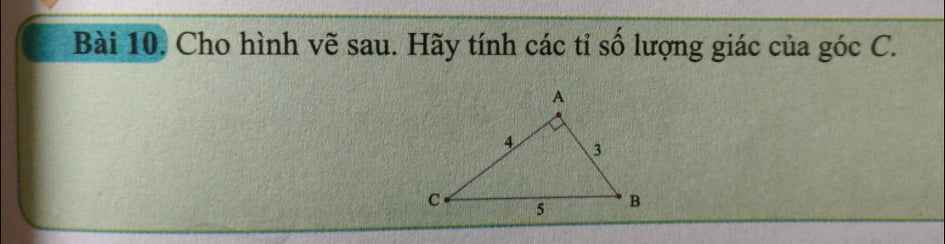 Giải giúp
Giải giúp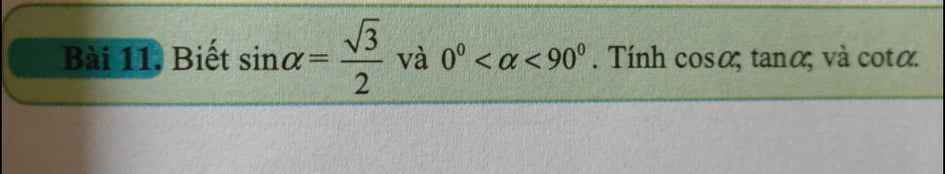 Giải giúp
Giải giúp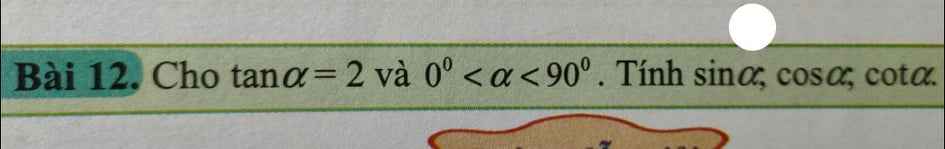 Giải giúp
Giải giúp Giải giúp
Giải giúp



