a) Ta có: \(AB^2+AC^2=5^2+12^2=169=13^2=BC^2\)
\(\Rightarrow\Delta ABC\) vuông tại A (Py-ta-go đảo)
tam giác ABC vuông tại A có đường cao AH nên áp dụng hệ thức lượng
\(\Rightarrow AH.BC=AB.AC\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{12.5}{13}=\dfrac{60}{13}\left(cm\right)\)
b) tam giác AHB vuông tại H có đường cao HE nên áp dụng hệ thức lượng
\(\Rightarrow AE.AB=AH^2\)
tam giác AHC vuông tại H có đường cao HF nên áp dụng hệ thức lượng
\(\Rightarrow AF.AC=AH^2\Rightarrow AE.AB=AF.AC\)
c) \(AE.AB=AF.AC\Rightarrow\dfrac{AE}{AC}=\dfrac{AF}{AB}\)
Xét \(\Delta AEF\) và \(\Delta ABC:\) Ta có: \(\left\{{}\begin{matrix}\angle BACchung\\\dfrac{AE}{AC}=\dfrac{AF}{AB}\end{matrix}\right.\)
\(\Rightarrow\Delta AEF\sim\Delta ABC\left(c-g-c\right)\)

 giải giúp
giải giúp


 giải giúp
giải giúp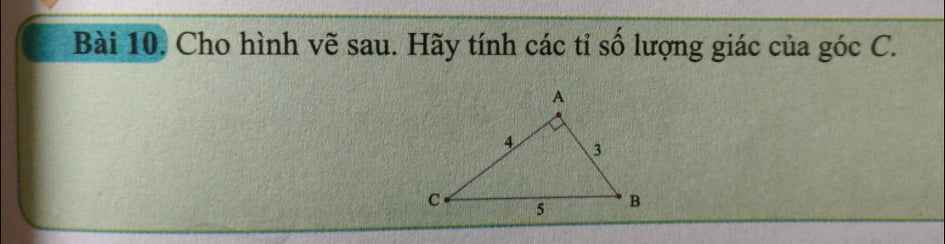 Giải giúp
Giải giúp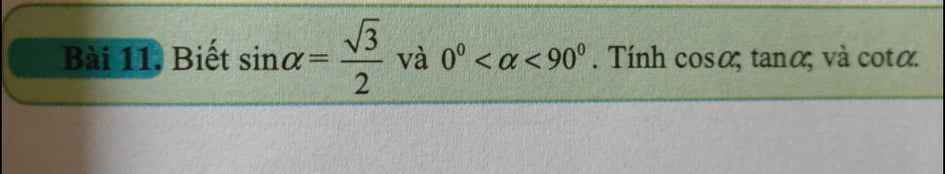 Giải giúp
Giải giúp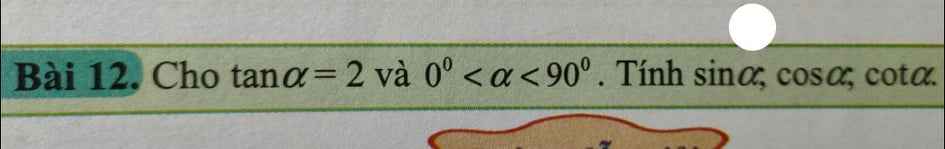 Giải giúp
Giải giúp Giải giúp
Giải giúp



