giả sử tam giác ABC vuông tại A có \(tanC=2\)
\(\Rightarrow\dfrac{AB}{AC}=2\Rightarrow AB=2AC\Rightarrow BC=\sqrt{AC^2+AB^2}\)
\(=\sqrt{AC^2+4AC^2}=\sqrt{5}AC\)
\(\Rightarrow sinC=\dfrac{AB}{BC}=\dfrac{2AC}{\sqrt{5}AC}=\dfrac{2}{\sqrt{5}}\Rightarrow sin\alpha=\dfrac{2}{\sqrt{5}}\)
\(cosC=\dfrac{AC}{BC}=\dfrac{AC}{\sqrt{5}AC}=\dfrac{1}{\sqrt{5}}\Rightarrow cos\alpha=\dfrac{1}{\sqrt{5}}\)
\(cotC=\dfrac{AC}{AB}=\dfrac{AC}{2AC}=\dfrac{1}{2}\Rightarrow cot\alpha=\dfrac{1}{2}\)
Ta có: \(\cot\alpha=\dfrac{1}{\tan\alpha}\)
nên \(\cot\alpha=\dfrac{1}{2}\)
Ta có: \(\sin\alpha=\dfrac{\tan\alpha}{\cot\alpha}\)
nên \(\sin\alpha=2:\dfrac{1}{2}=4\)
Ta có: \(\cos\alpha=\dfrac{\cot\alpha}{\tan\alpha}\)
nên \(\cos=\dfrac{1}{2}:2=\dfrac{1}{4}\)

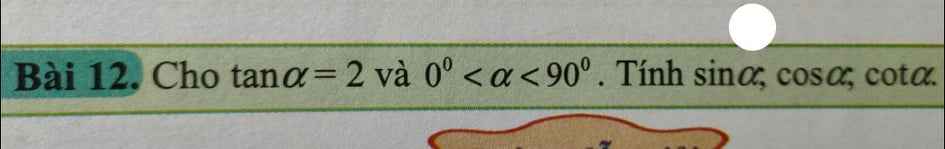 Giải giúp
Giải giúp







 giải giúp
giải giúp giải giúp
giải giúp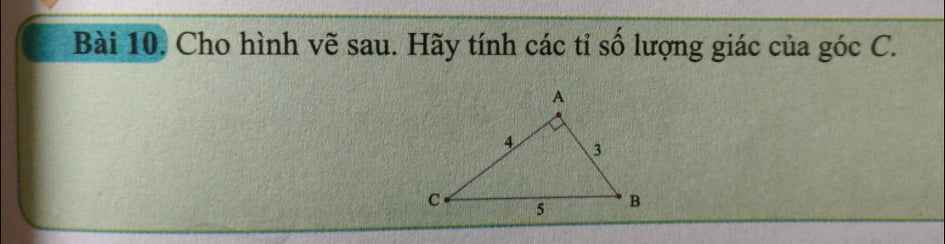 Giải giúp
Giải giúp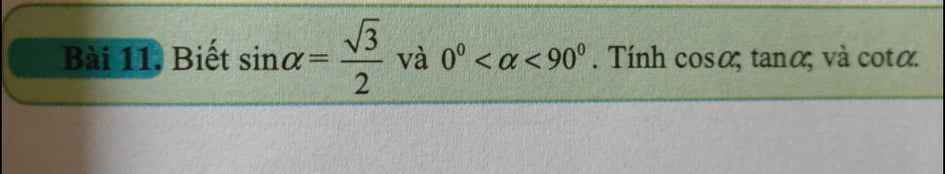 Giải giúp
Giải giúp Giải giúp
Giải giúp



