\(y'=\dfrac{cosx}{sinx}\), \(y''=-\dfrac{1}{sin^2x}\).
Vì vậy:
\(y'+y''.sinx+tanx=\dfrac{cosx}{sinx}+\dfrac{-1}{sin^2x}.sinx+\dfrac{sinx}{cosx}\)
\(=\dfrac{cosx}{sinx}+\dfrac{-1}{sinx}+\dfrac{sinx}{cosx}\)
\(=\dfrac{cosx-1}{sinx}+\dfrac{sinx}{cosx}\)\(=\dfrac{cos^2x+sin^2x-cosx}{sinx.cosx}=\dfrac{1-cosx}{sinx.cosx}\).
Bạn xem lại đề nhé.
Chứng minh rằng hàm số sau đây thỏa mãn hệ thức tương ứng đã cho :
Nếu \(y=x^{\sin x}\) thì \(y'\cos x-y\sin x-y"=0\)
Chứng minh hàm số sau đây thỏa mãn hệ thức :
Nếu \(y=\frac{1+\ln x}{x\left(1-\ln x\right)}\) thì \(y'=\frac{2xy}{x^2+1}+e^x\left(x^2+1\right)\)
Tính đạo hàm của các hàm số sau:
g) \(y = \ln (x^2+x+1)\)
l) \(y = \dfrac{\ln x}{x+1}\)
giải hệ
\(\left\{{}\begin{matrix}y\left[log_2\left(x-3\right)+log_3y\right]=x+1\\x^3-3x-y^3-6y^2-9y-2+ln\dfrac{x-1}{y+1}=0\end{matrix}\right.\)
Giải hệ phương trình sau :
\(\begin{cases}x+y=30\\\ln x+\ln y=3\ln6\end{cases}\)
a)Xác định điểm I thuộc đồ thị (C) của hàm số đã cho biết rằng hoành độ của điểm I là nghiệm của Phương trình f’’(x)= 0.
b)Viết công thức chuyển hệ tọa độ trong phép tịnh tiến vectơ OI và viết Phương trình của đường cong với hệ tọa độ IXY. Từ đó suy ra bằng I là tâm đối xứng đường cong (C).
c)Viết phương trình tiếp tuyến của đường cong (C) tại điểm I đối với hện tọa độ Oxy. Chứng minh rằng trên khoảng (-∞;1) đường cong (C) nằm phía dưới tiếp tuyến tại I của (C) và trên khoảng (1; +∞) đường cong (C) nằm phía trên tiếp tuyến đó.
Cho \(x\), \(y\), \(z\) \(\in\left[0;2\right]\) và thỏa mãn \(x+2y+z=6\). Tìm giá trị lớn nhất của biểu thức \(P=3^{2x-x^2}+5^{2y-y^2}+3^z+2x^2+4y^2\)
A. \(maxP=25\) B. \(maxP=26\)
C. \(maxP=27\) D. \(maxP=30\)
Mình cần bài giải ạ, mình cảm ơn nhiều♥
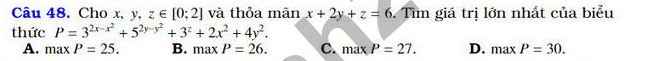
Cho x là số nguyên dương và y là số thực. Có tất cả bao nhiêu cặp số \(\left(x;y\right)\) thỏa mãn \(ln\left(1+x+2y\right)=2y+3x-10\) ?
