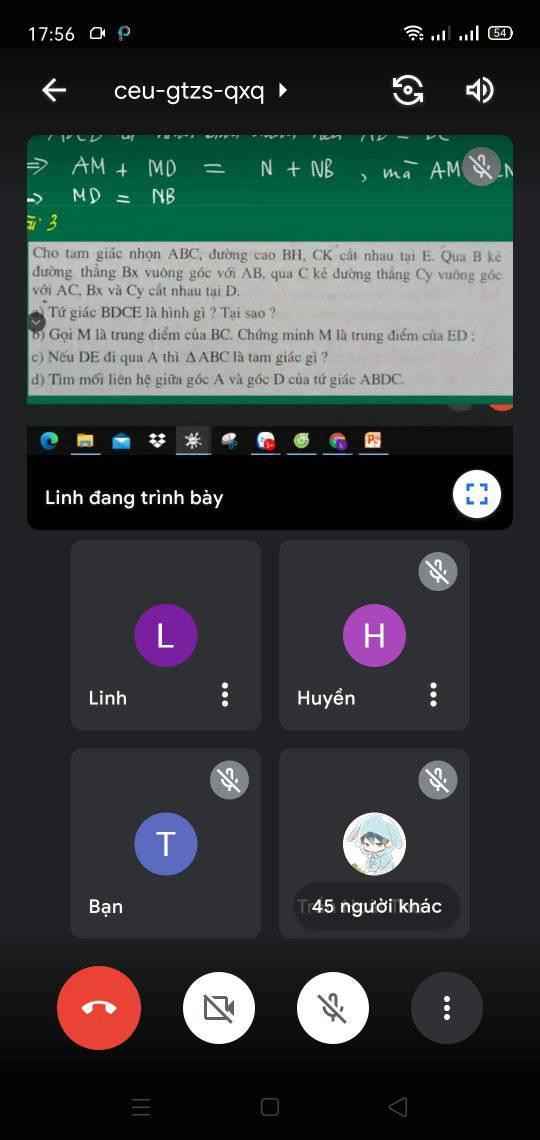
a) Xét tứ giác BDCE có:
BD//CE(cùng vuông góc AB)
BE//CD(cùng vuông góc AC)
=> BDCE là hình bình hành
b) Ta có: BDCE là hình bình hành
=> 2 đường chéo cắt nhau tại trung điểm mỗi đường
Mà M là trung điểm BC
=> M là trung điểm DE
c) Gỉa sử DE đi qua A
Xét tam giác ABD và tam giác ACD lần lượt vuông tại B và C có:
AD chung
\(\widehat{ADB}=\widehat{ADC}\)(BDCE là hình bình hành)
=> ΔABD=ΔACD(ch-gn)
=> AB=AC
=> Tam giác ABC cân tại A
d) Xét tứ giác ABCD có:
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\)(tổng 4 góc trong tứ giác)
\(\Rightarrow\widehat{A}=360^0-\widehat{B}-\widehat{C}-\widehat{D}\)
\(\Rightarrow\widehat{A}=360^0-90^0-90^0-\widehat{D}=180^0-\widehat{D}\)