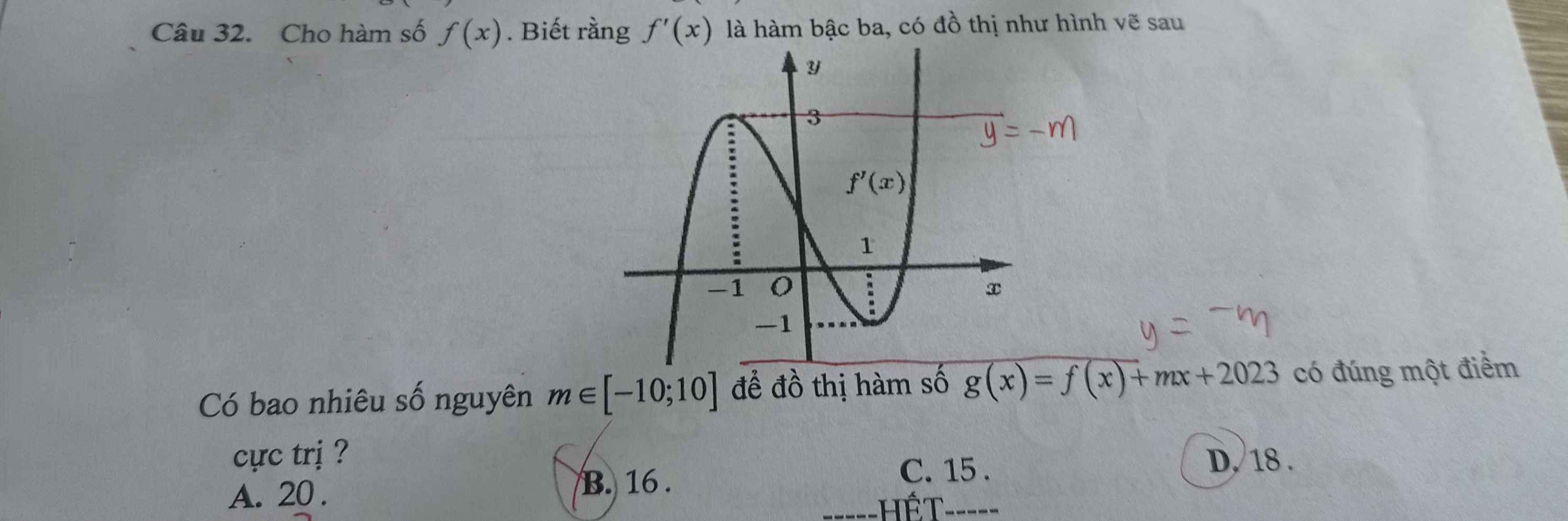Hàm có đúng 1 điểm cực trị khi \(g'\left(x\right)=0\) có đúng 1 nghiệm bội lẻ
\(\Rightarrow f'\left(x\right)+m=0\) có đúng 1 nghiệm bội lẻ
\(\Rightarrow f'\left(x\right)=-m\) có đúng 1 nghiệm bội lẻ
Từ đồ thị \(f'\left(x\right)\) ta suy ra: \(\left[{}\begin{matrix}-m\ge3\\-m\le-1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}m\le-3\\m\ge1\end{matrix}\right.\)
\(\Rightarrow\) Có 18 giá trị nguyên của m trong đoạn đã cho thỏa mãn
Đúng 1
Bình luận (0)
