Question

Giải các phương trình sau :

a) \(\sin^2\dfrac{x}{2}-2\cos\dfrac{x}{2}+2=0\)

b) \(8\cos^2x+2\sin x-7=0\)

c) \(2\tan^2c+3\tan x+1=0\)

d) \(\tan x-2\cos x+1=0\)

Answer 1

a) Đặt t = cos, t ∈ [-1 ; 1] thì phương trình trở thành

(1 - t²) - 2t + 2 = 0 ⇔ t² + 2t -3 = 0 ⇔

Phương trình đã cho tương đương với

cos = 1 ⇔ = k2π ⇔ x = 4kπ, k ∈ Z.

b) Đặt t = sinx, t ∈ [-1 ; 1] thì phương trình trở thành

8(1 - t²) + 2t - 7 = 0 ⇔ 8t² - 2t - 1 = 0 ⇔ t ∈ {}.

Các nghiệm của phương trình đã cho là nghiệm của hai phương trình sau :

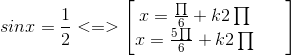
và

Đáp số : x = + k2π; x = + k2π;

x = arcsin() + k2π; x = π - arcsin() + k2π, k ∈ Z.

c) Đặt t = tanx thì phương trình trở thành 2t² + 3t + 1 = 0 ⇔ t ∈ {-1 ; }.

Vậy

d) Đặt t = tanx thì phương trình trở thành

t - + 1 = 0 ⇔ t² + t - 2 = 0 ⇔ t ∈ {1 ; -2}.

Vậy