+) Nếu \(a\ge0\) \(\Rightarrow\sqrt{128a^2}=8a\sqrt{2}\)
+) Nếu \(a< 0\) \(\Rightarrow\sqrt{128a^2}=-8a\sqrt{2}\)
Đúng 0
Bình luận (0)
Bài 1: Căn bậc hai
Các câu hỏi tương tự
Đưa thừa số ra ngoài dấu căn: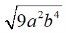
Đưa thừa số ra ngoài dấu căn :
a. \(\sqrt{9\text{6}}.\sqrt{\text{1}2\text{5}}\)
b.\(\sqrt{a^4.\text{6}^{\text{5}}}\)
c.\(\sqrt{a^{\text{6}}.b^{\text{1}\text{1}}}\)
d.\(\:\sqrt{a^{\text{3}}\left(\text{1}-a\right)^4}\)
Chứng minh rằng: \(\frac{1}{4}< \frac{\sqrt{2+\sqrt{2+\sqrt{2+...+\sqrt{2}}}}}{\sqrt{2+\sqrt{2+\sqrt{2+...+\sqrt{2}}}}}< \frac{3}{10}\)( ở tử có n dấu căn, ở mẫu có n - 1 dấu căn)
Chứng minh rằng: \(\frac{1}{4}< \frac{\sqrt{2+\sqrt{2+\sqrt{2+...+\sqrt{2}}}}}{\sqrt{2+\sqrt{2+\sqrt{2+...+\sqrt{2}}}}}< \frac{3}{10}\)( ở tử có n dấu căn, ở mẫu có n-1 dấu căn)
Ai giúp mình với huhu :(
\(\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2+......}}}}\) ( n dấu căn)
Cho
S= \(\dfrac{2-\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2+...+\sqrt{2}}}}}}{2-\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2+...+\sqrt{2}}}}}}\)
Trên tử của S có n dấu căn
Dưới mẫu của S có n-1 dấu căn
CMR 0,25 < S < 0,3
Giúp mình nha!
Chứng minh\(\sqrt{3+\sqrt{3+......+\sqrt{3}}}\)( 2019 dấu căn ) < 2
Đưa thừa số ra ngoài dấu căn:
a)√96.125
b)√a^4 b^5
c)a^6 b^11
d)a^3(1-4)^4 (a>1)
Giúp mình
Sqrt(2+Sqrt(((5+Sqrt(5))/(2))))+Sqrt(2-Sqrt(((5+Sqrt(5))/(2))))-Sqrt(3-Sqrt(5))
Mình không biết tạo căn bậc hai , sao chép cái nó ra như vậy,dịch là (căn bậc hai của 2 cộng căn bậc hai của 5+căn 5 chia 2 tất cả trừ căn bậc hai của 2 trừ căn bậc hai của 5+căn 5 chia 2 tất cả trừ căn bậc hai của 3 căn 5)😂