Ta có: E = Eđ + Et ![]() Eđ = E – Et với cơ năng
Eđ = E – Et với cơ năng 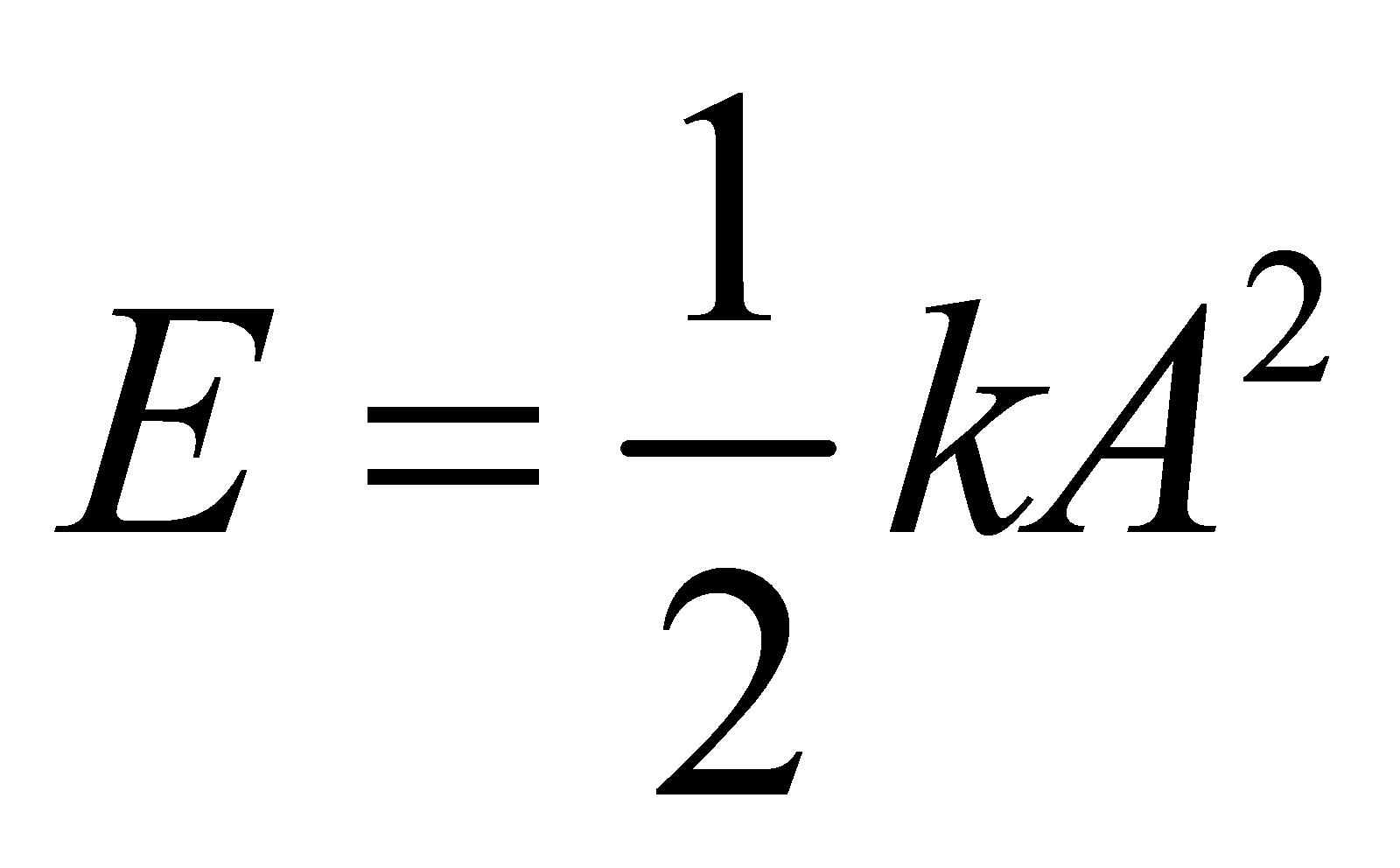 và thế năng
và thế năng 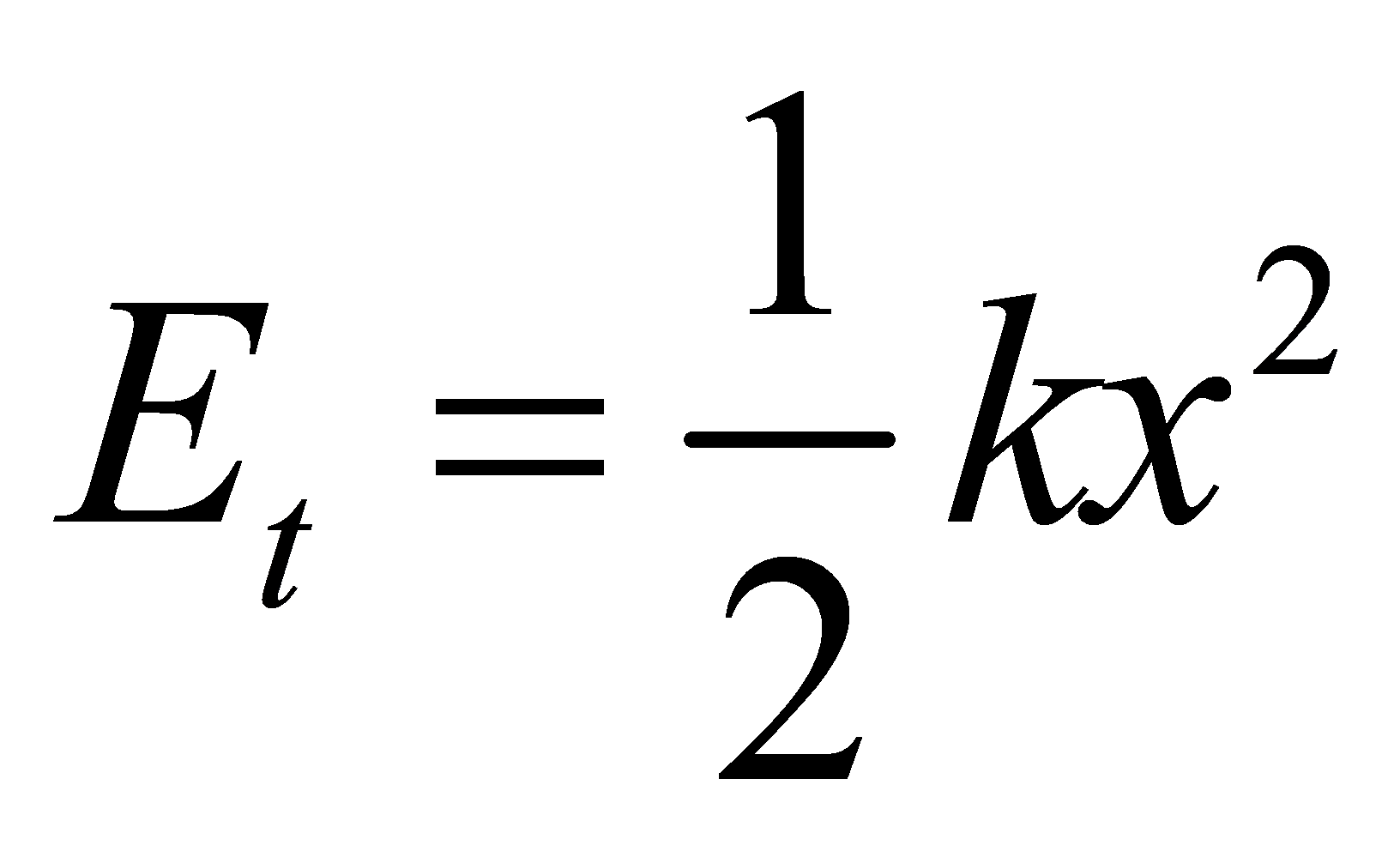 Động năng E đ =
Động năng E đ = ![]() .20(0,042 – 0,032) = 0,007J.
.20(0,042 – 0,032) = 0,007J.
Ta có: E = Eđ + Et ![]() Eđ = E – Et với cơ năng
Eđ = E – Et với cơ năng 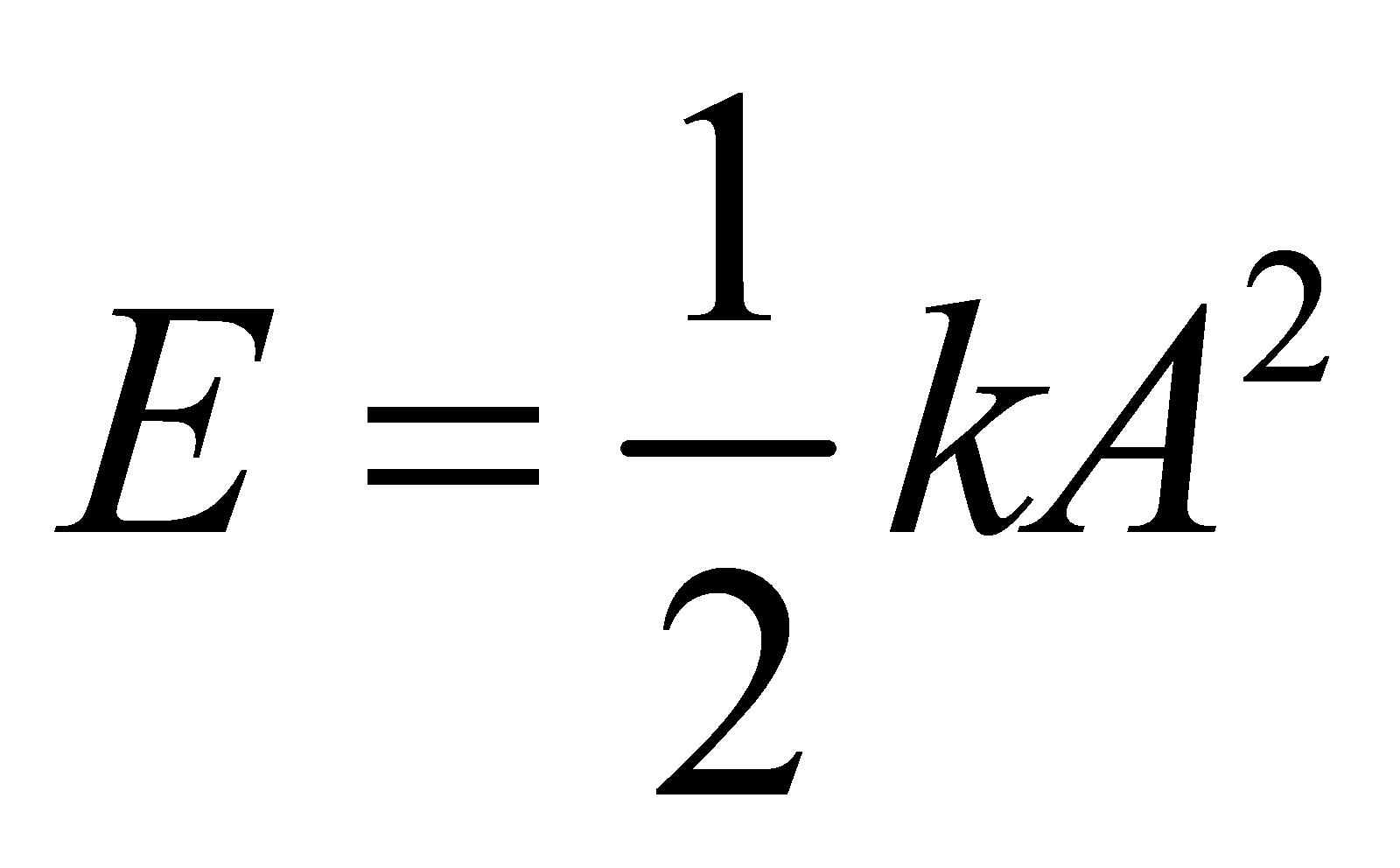 và thế năng
và thế năng 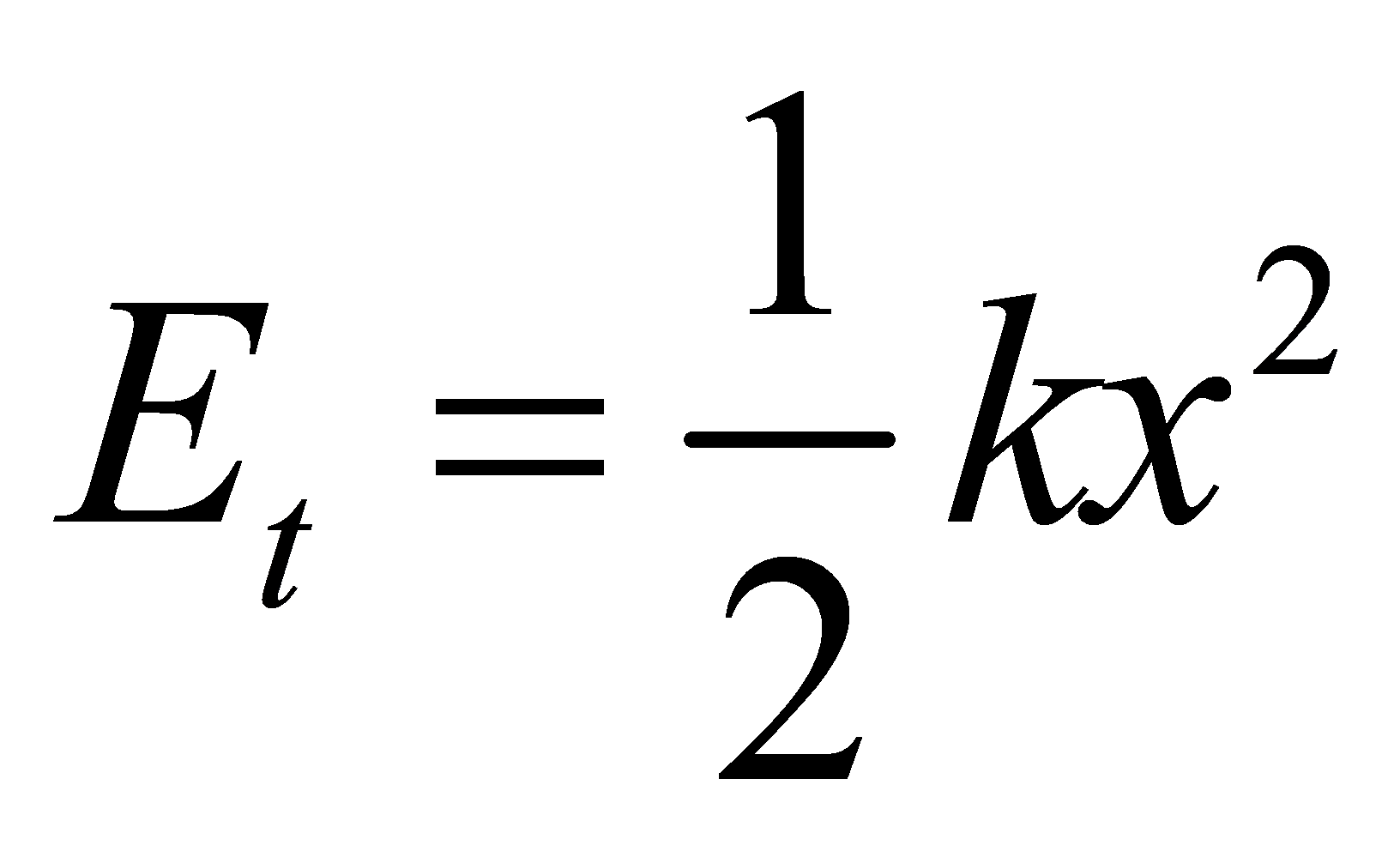 Động năng E đ =
Động năng E đ = ![]() .20(0,042 – 0,032) = 0,007J.
.20(0,042 – 0,032) = 0,007J.
Con lắc lò xo gồm vật có khối lượng m gắn vào lò xo có độ cứng k đặt nằm ngang dao động điều hòa, mốc thế năng ở vị trí cân bằng. khi thế năng bằng 1/3 động năng thì tỉ số độ lớn giữa lực đàn hồi và lực đàn hồi cực đại là bao nhiêu?
Một con lắc lò xo treo thẳng đứng gồm lò xo có độ cứng k = 50N/m và vật có khối lượng m (g) dao động điều hòa theo phương thẳng đứng với li độ \(x=10\cos\left(5\pi t+\dfrac{\pi}{2}\right)\left(cm\right)\) biết g = 10 m/s2.
a) Tính khối lượng của vật và chu kỳ của con lắc
b) Tính thế năng, động năng và cơ năng của con lắc khi vật ở li độ x = 2 cm
c) Tính lực đàn hội của lò xo khi vật nặng có \(v=\dfrac{1}{2}v_{max}\)
Một con lắc lò xo gồm lò xo nhẹ có độ cứng 100 N/m và vật nhỏ khối lượng m. Con lắc dao động điều hòa với chu kì T với biên độ 10 cm. Biết ở thời điểm t vật ở vị trí M. Ở thời điểm t + \(\dfrac{5T}{6}\), vật lại ở vị trí M nhưng đi theo chiều ngược lại. Động năng của vật khi nó ở M là:
Một con lắc lò xo (độ cứng của lò xo là 50 N/m) dao động điều hòa theo phương
ngang. Cứ sau 0,05 s thì vật nặng của con lắc lại cách vị trí cân bằng một khoảng như cũ. Lấy π\(^2\)\(=\)10. Khối lượng vật nặng của con lắc bằng
Con lắc lò xo treo thẳng đứng, khi vật ở VTCB thì lò xo giãn 3cm. Kích thích cho vật dao động với biên độ A=6cm thì trong 1 chu kì dao động T, khoảng thời gian lò xo bị nén là :
A. T/12
B. T/3
C.2T/3
D.T/6
Một con lắc lò xo treo thẳng đứng (lấy g = 10 m/s\(^2\)) quả cầu có khối lượng 200 g dao động điều hòa với cơ năng dao động 0,08 J. Khi lò xo có chiều dài 28 cm thì vận tốc bằng không và lúc đó lực đàn hồi có độ lớn 2 N. Chiều dài tự nhiên của lò xo là
Một con lắc lò xo dao động điều hòa với phương trình x = Acos2(\(\pi t+\dfrac{\pi}{3}\)). Động năng và thế năng của con lắc biến thiên tuần hoàn với chu kỳ là bao nhiêu?
Quả cầu của một con lắc lò xo dao động với biên độ A = 3 cm, khi qua vị trí cân bằng có vận tốc 0,6 m/s, sẽ có chu kỳ dao động là:
Một con lắc lò xo dao động điều hòa theo phương ngang với tần số góc . Vật nhỏ của con lắc có khối lượng 100 g. Tại thời điểm t = 0, vật nhỏ qua vị trí cân bằng theo chiều dương. Tại thời điểm t = 24173/60 s, vận tốc v và li độ x của vật thỏa mãn \(v=\left(2-\sqrt{3}\right)\omega x\) lần thứ 2015. Lấy \(\pi^2=10\). Độ cứng của lò xo là
Một con lắc lò xo gồm lò xo nhẹ nằm ngang và mặt phẳng M. Con lắc dao động điều hòa trên trục Ox, chiều dài của lò xo thay đổi từ 20cm đến 30cm. Ở vị trí lò xo dài 30cm, độ lớn gia tốc của vật M là 8m/s2. Chọn gốc tọa độ O tại vị trí cân bằng, gốc thời gian là lúc vật M đi qua O theo chiều âm. Lấy \(\pi^2=10\)
a) Viết phương trình dao động của vật M
b) Xác định vị trí vật M khi con lắc có động năng bằng ba lần thế năng
c) Biết hiệu giữa quãng đường lớn nhất và quảng đường nhỏ nhất (vật M đi được trong cùng một khoảng thời gian \(\Delta t\)) đạt cực đại. Tính \(\Delta t\)
d) Một vật nhỏ N dao động trên trục Oy với phương trình \(y=10cos\left(4\pi t-\dfrac{\pi}{6}\right)cm\) (Ox và Oy vuông góc với nhau, O là vị trí cân bằng của cả vật N và vật M). Xác định khoảng cách giữa vật M và vật N khi vật M có li độ \(x=-2,5\sqrt{3}cm\) và đang chuyển động theo chiều âm