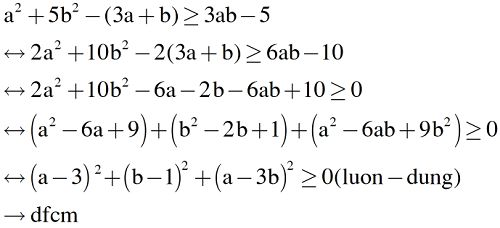Violympic toán 8
Các câu hỏi tương tự
Cho a2 - b2= 4c2. Chứng minh rằng: (5a - 3b + 8c).(5a - 3b - 8c) = (3a - 5b)2
Biết a3-3ab2=5 và b3-3a2b=10.Tính M=\(\frac{a^2+b^2}{2018}\)
Cho biết a3 - 3ab2= 5 và b3 - 3a2b= 10. Tính S= 2018a2 + 2018b2
Cho \(a^3-3ab^2=5\) và \(b^3-3a^2b=10\). Tính S = \(2019a^2+2019b^2\)
Cho các số thực dương a,b,c. Chứng minh rằng :
\(\frac{1}{3a+2b+4c}+\frac{1}{3b+2c+4a}+\frac{1}{3c+2a+4b}\)< \(\frac{1}{a+3b+5c}+\frac{1}{b+3c+5c}+\frac{1}{c+3a+5b}\)
Biết \(b\ne\pm3a\) và \(6a^2-15ab+5b^2=0\) tính giá trị của
Q = \(\dfrac{2a-b}{3a-b}+\dfrac{5b-a}{3a+b}\)
Cho a3 + 3ab2 = 63 và b3 + 3a2b = 62. Tính giá trị M = a2 - b2
So sánh
a) cho a<b. So sánh 3a-2 và 3b-2; 3a-2 và 3b+1
b) Cho -5a+1>=-5b+1. So sánh a và b
a3-3a2+5a-2011=b3-3b2 +5b+2005
a+b=?