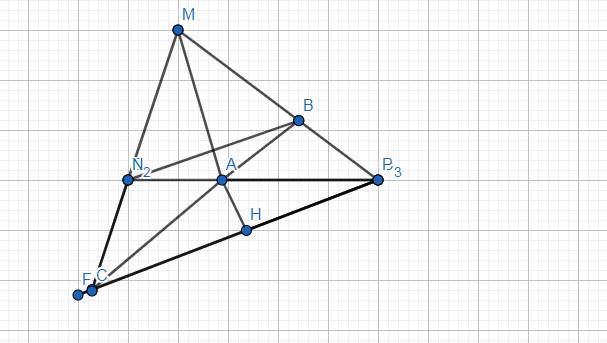
Bổ sung đề: MO cắt NP tại A. Trên tia MN, lấy C sao cho MC=MP. Chứng minh B,A,C thẳng hàng
Xét ΔMNO và ΔMBO có
MN=MB
ON=OB
MO chung
Do đó: ΔMNO=ΔMBO
=>\(\hat{NMO}=\hat{BMO}\)
Xét ΔMNA và ΔMBA có
MN=MB
\(\hat{NMA}=\hat{BMA}\)
MA chung
Do đó: ΔMNA=ΔMBA
=>\(\hat{MNA}=\hat{MBA}\)
mà \(\hat{MNA}+\hat{ANC}=180^0\) (hai góc kề bù)
và \(\hat{MBA}+\hat{ABP}=180^0\) (hai góc kề bù)
nên \(\hat{ANC}=\hat{ABP}\)
Ta có: ΔMNA=ΔMBA
=>AN=AB
Ta có: MN+NC=MC
MB+BP=MP
mà MN=MB và MC=MP
nên NC=BP
Xét ΔANC và ΔABP có
AN=AB
\(\hat{ANC}=\hat{ABP}\)
NC=BP
Do đó: ΔANC=ΔABP
=>\(\hat{NAC}=\hat{BAP}\)
mà \(\hat{BAP}+\hat{BAN}=180^0\) (hai góc kề bù)
nên \(\hat{BAN}+\hat{CAN}=180^0\)
=>B,A,C thẳng hàng