a,Xét tứ giác AEMF có:
E^=90o
A^=90o
F^=90o
=>AEDF là hình chữ nhật
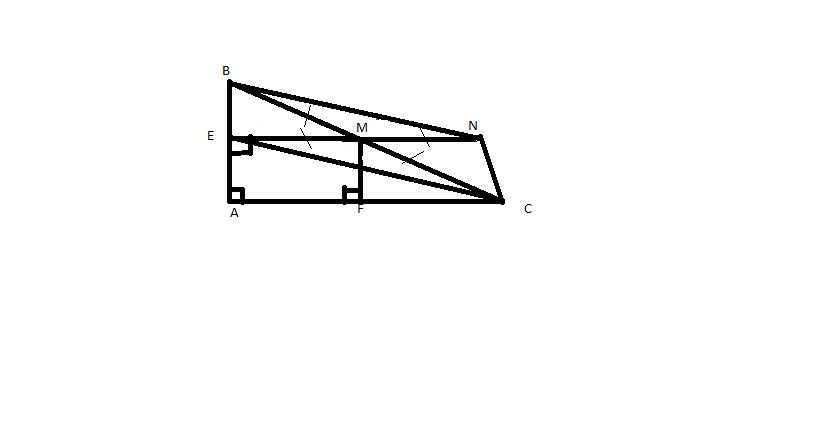
a: Xét tứ giác AEMF có
góc AEM=góc AFM=góc FAE=90 độ
nên AEMF là hình chữ nhật
b: Xét tứ giác BECN có
M là trung điểm chung của BC và EN
nên BECN là hình bình hành
a,Xét tứ giác AEMF có:
E^=90o
A^=90o
F^=90o
=>AEDF là hình chữ nhật

a: Xét tứ giác AEMF có
góc AEM=góc AFM=góc FAE=90 độ
nên AEMF là hình chữ nhật
b: Xét tứ giác BECN có
M là trung điểm chung của BC và EN
nên BECN là hình bình hành
3: Cho ∆ABC vuông tại A (AB<AC) có AM là đường trung tuyến . E,F lần lượt là hình chiếu của M trên AB,AC
a)Chứng minh : Tứ giác AEMF là hình chữ nhật
b)Vẽ K đối xứng với F qua M . Chứng minh : Tứ giác BKCF là hình bình hành.
Cho tam giác ABC vuông tại A (AB<AC). Lấy M,E lần lượt là trung điểm cạnh BC, kẻ MD vuông góc với AB tại D, kẻ ME vuông góc với AC tại E.
a) Chứng minh ADME là hình chữ nhật
b) Chứng minh DBME là hình bình hành
c) Kẻ đường cao AH của tam giác ABC. Chứng minh DEMH là hình thang cân
Cho tam giác ABC vuông tại A. Gọi M là trung điểm của BC, E là điểm đối xứng của A qua M.
a) CMR: ABEC là hình chữ nhật.
b) Tam giác ABC phải có thêm điều kiện gì để ABEC là hình vuông?
cho tam giác ABC vuông tại A, gọi I là trung điểm của BC, Từ I kẻ IM vuông góc AB ( M thuộc AB), kẻ IN vuông góc AC (N thuộc AC)
a) chứng minh tứ giác AMIN là hình hình chữ nhật
b) gọi D là điểm đối xứng với a qua I. Tứ giác ABDC là hình gì
c) tìm điều kiện của tam giác ABC để hình chữ nhật AMIN là hình vuông
Cho tam giác ABC vuông tại A. Qua B kẻ Bx vuông góc với AB, qua C kẻ Cy vuông góc AC. Gọi D là giao điểm của Bx và Cy.
a) Chứng minh tứ giác ABDC là hình chữ nhật.
b) Vẽ M đối xứng với B qua A, N đối xứng với C qua A. Chứng minh tứ giác BCMN là hình thoi và AD = MC.
c) Gọi E, F thứ tự là trung điểm của AC và MN. Chứng minh EF// ND.
Bài 7. Cho cân tại A, AM là đường cao. Gọi N là trung điểm của AC. D là điểm đối xứng của M qua N.
a) CMR: Tứ giác ADCM là hình chữ nhật.
b) CMR: Tứ giác ABMD là hình bình hành và BD đi qua trung điểm O của AM.
c) BD cắt AC tại I. CMR: DI=2/3OB
Giúp mik với
Cho tam giác vuông ABC (A = 90°). Lấy M bất kì trên cạnh BC. Gọi E, F lần lượt là các điểm đối xứng với M qua AB và AC. Gọi I, K lần lượt là giao điểm của MẸ với AB và MF với AC. Chứng minh:
a) MIAK là hình chữ nhật.
b) A là trung điểm của EF.