a: Xét tứ giác ABCD có
M là trung điểm của AC
M là trung điểm của BD
Do đó; ABCD là hình bình hành
Suy ra: AB//CD và AB=CD
b: Xét ΔBAK vuông tại A và ΔDCK vuông tại C có
BA=DC
AK=KC
Do đó: ΔBAK=ΔDCK
Suy ra: KB=KD
=>KG=KN
a: Xét tứ giác ABCD có
M là trung điểm của AC
M là trung điểm của BD
Do đó; ABCD là hình bình hành
Suy ra: AB//CD và AB=CD
b: Xét ΔBAK vuông tại A và ΔDCK vuông tại C có
BA=DC
AK=KC
Do đó: ΔBAK=ΔDCK
Suy ra: KB=KD
=>KG=KN
Câu 3: (4,0 điểm) Cho tam giác đều ABC, đường trung tuyến AM . Trên tia đối
tia CB lấy điểm D sao cho CD = CB. Vẽ CH L AD (He 4D)
a) Chứng minh : H là trung điểm của AD
b) Chứng minh: AABD vuông tại A.
c) Tia đối tia CH và tia AM cắt nhau tại P. Chứng minh: Điểm C là trọng tâm
của tam giác APD.
d) Biết AB = 10 cm . Tính AM (ghi kết quả đúng không làm tròn số )
Cho ∆abc vuông tại a có ab=6cm, ac=8cm. Tia phân giác của góc abc cắt ac tại d.
a)Tính bc
b) Kẻ ah vuông góc với bc, tia ah cắt bc tại k. Chứng minh:∆ahb=∆khb
c) Chứng minh:dk vuông góc với bc
d) Qua c kẻ đường thẳng song song với ak, cắt tia ba tại e. Chứng minh:2(ad+ae)>ec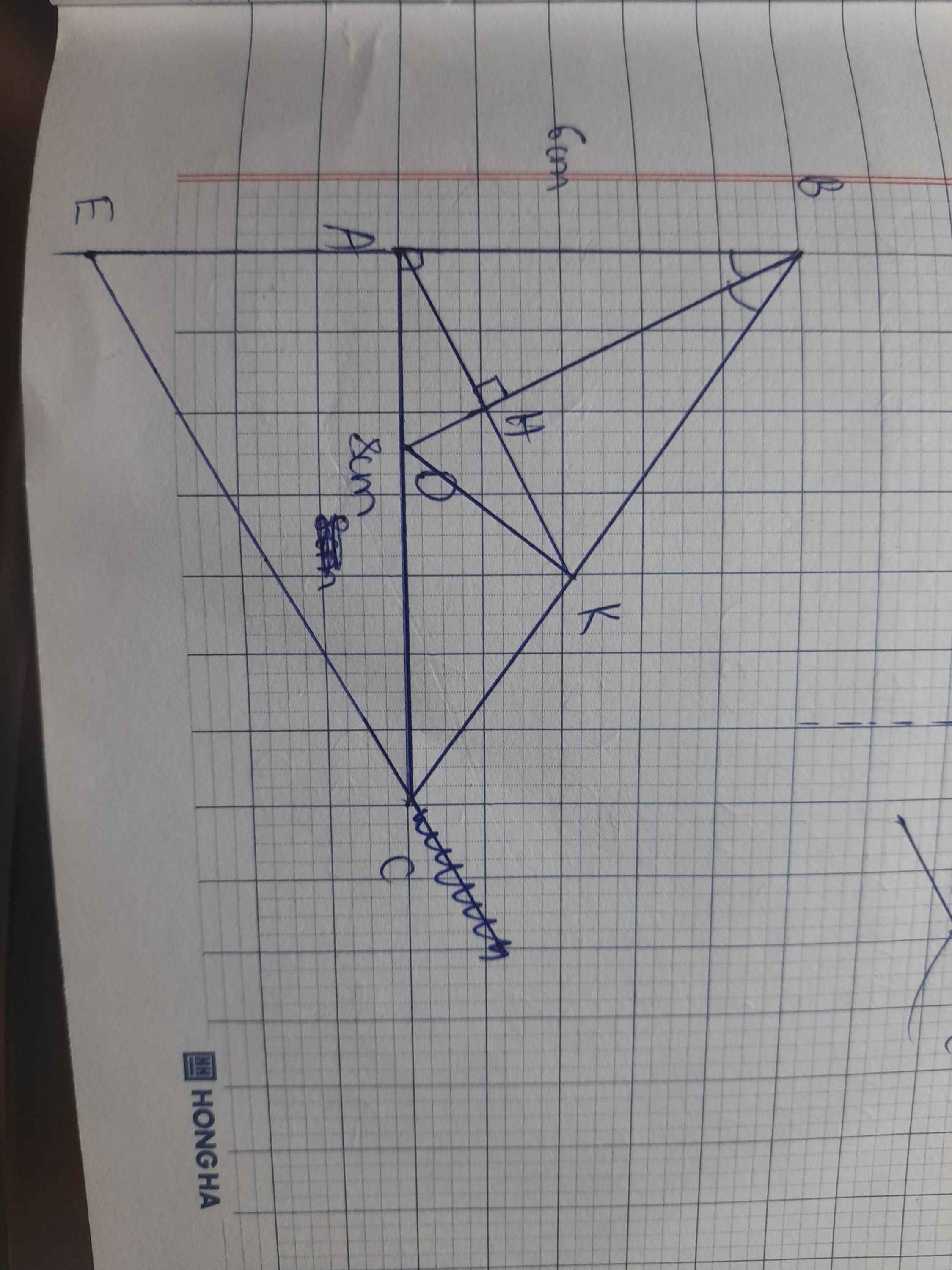
Cho tam giác ABC vuông tại A, AK là đường cao. Gọi M,N lần lượt là hình chiếu của K trên AB, AC. Gọi D là trung điểm AB và I là điểm đối xứng của A qua K. Chứng minh CD vuông góc IN
Cho tam giác ABC, AB<AC, trên tia BA và CA lần lượt lấy M và N sao cho BM=CN, trên cạnh AC lấy điểm D sao cho CD=AB. Chứng minh rằng: Ba đường trung trực của AD,MN,BC cùng đi qua một điểm
Cho tam giác ABC vuông tại A, có AB > AC. Trên tia đối của tia CA lấy điểm D
\nsao cho C là trung điểm của đoạn thẳng AD. Qua C dựng đường vuông góc với AD cắt
\ncạnh BD tại E.
\na) Chứng minh tam giác AED là tam giác cân.
\nb) Chứng minh AE là trung tuyến của tam giác ABD.
\nc) Phân giác góc BEA cắt cạnh AB tại F. Gọi G là giao điểm của AE và BC. Chứng minh
\nba điểm D, G, F thẳng hàng.Cho tam giác ABC vuông tại A, có AB > AC. Trên tia đối của tia CA lấy điểm D
\nsao cho C là trung điểm của đoạn thẳng AD. Qua C dựng đường vuông góc với AD cắt
\ncạnh BD tại E.
\na) Chứng minh tam giác AED là tam giác cân.
\nb) Chứng minh AE là trung tuyến của tam giác ABD.
\nc) Phân giác góc BEA cắt cạnh AB tại F. Gọi G là giao điểm của AE và BC. Chứng minh
\nba điểm D, G, F thẳng hàng.
cho tam giác abc vuông tại a có bc=2ab. tia phân giác góc b cắt ac tại .a, chứng minh bd=cd b, tính góc b và góc c của tam giác abc
Bài 1: Cho tam giác ABC. Đường cao AD. Kẻ DL vuông AB. Trên tia DL lấy điểm M,
sao cho AB là trung trực của DM. Kẻ DK vuông AC. Trên tia DK lấy điểm N sao cho AC
là trung trực của DN. MN giao AB tại F và giao AC tại E. CMR:
a, Tam giác MAN cân.
b, DA là phân giác của góc FDE.
c, AD,BE,CF đồng quy.
d, H là trực tâm của tam giác ABC (H là giao điểm của BE, CF)
mình đang cần gấp ạ
Bài 4:Cho tam giác abc vuông tại A.Từ C kẻ Cx vuông góc với BC,gọi F là giao điểm của Cx và phân giác góc ABC,BF cắt AC tại E.Kẻ CD vuông góc với EF tại D,kéo dài BA cắt CD tại S
a)Chứng minh CD là phân giác góc ECF
b)DE=DF và SE//CFF
Bài 5:Cho tam giác ABC cân tại A,góc A nhọn,đường phân giác AD.Trên tia đối tia DC lấy điểm M sao cho MD=ADD
a)Chứng minh tam giác ADM vuông cân
b)Kẻ BN vuông góc AM tại N,BN cắt AD tại O,chứng minh OM vuông góc ABB
c)Chứng minh OB=OC; AM//OC
Bài 6:Cho tam giác ABC vuông tại A(AB<AC),đường cao AHH,trên cạnh BC lấy điểm M sao cho BA=BMM
a)Chứng minh AM là phân giác của góc HAC
b)Gọi K là hình chiếu vuông góc của M trên AC,chứng minh AM là đường trung trực HK
c)I là hình chiếu vuông góc của C trên AM,chứng minh AH,KM,CI cùng đi qua 1 điểm
Vẽ hình luôn giúp mình
cho tam giác abc có ba góc nhọn đường cao AH trên một nửa MP thẳng bờ lại đường thẳng a có chứa điểm b kẻ CX song song AD trên tia ax lấy điểm D sao cho CD = AB kẻ DK vuông góc BC k thuộc D sao cho CD = AB kể DK vuông góc BC ê k thuộc BC
a) AH= DK
b)CA=CD
C)AC song song BD