Ta có 
vuông cân 
vuông cân 
Theo giải thiết 
Lại có 
là hình bình hành
Mặt khác 
là hình chữ nhật
Đúng 0
Bình luận (0)
Tứ giác
Các câu hỏi tương tự
19 tháng 10 2023 lúc 23:15
Cho hình bình hành ABCD. Gọi o là giao điểm hai đường thẳng ac và bd. Qua điểm O vẽ đường thẳng song song với AB cắt hai cạnh AD, BC lần lượt tại M, N. Trên AB, CD lần lượt lấy các điểm P, Q sao cho AP = CQ. Chứng minh:
a) Các tứ giác AMNB, APCQ là hình bình hành
b) MP // NQ; MQ = NP
11 tháng 11 2017 lúc 22:40
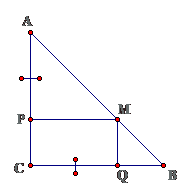
Cho tam giác ABC vuông cân tại C. Trên các cạnh AC, BC lấy lần lượt các điểm P, Q sao cho AP = CQ. Từ P vẽ PM // BC
a) CM : PCQM là hình chữ nhật
b) Gọi I là trung điểm của PQ. Cm khi P di chuyển trên AC, Q di chuyển trên BC thì I di chuyển trên một đoạn thẳng cố định
Help <3
Cho tam giác cân BCD cân tại C, lấy điểm Q trên cạnh BC sao cho QB = QC và lấy điểm P trên cạnh CD sao cho PC = PD. Chứng minh rằng:
a. CQ= CP. Từ đó suy ra tam giác CQP là tam giác gì? Vì sao?
b. QP//BD . Từ đó cho biết tứ giác QPDB là hình gì?
c. Tính các góc còn lại trong tứ giác QPDB biết B = 60⁰.
d. Tính cạnh BD biết QP = 4 cm.
Cho tam giác ABC vuông tại A. Gọi M, N, P lần lượt là trung điểm của ab ac bc. Gọi D, E lần lượt là điểm đối xứng của P qua M và N.a, Tính AP và diện tích tam giác ABC biết AB 6cm, AC 8cm.b, Chứng minh tứ giác AMPN là hình chữ nhật.c, Chúng minh tứ giác APCE là hình thoi.d, Tam giác ABC cần có điều kiện gì để tứ giác APCE là hình vuông?e, Chứng minh AP, BE, CD đồng quy.f, Chứng minh ba điểm D, A, E thẳng hàng.
Đọc tiếp
Cho tam giác ABC vuông tại A. Gọi M, N, P lần lượt là trung điểm của ab ac bc. Gọi D, E lần lượt là điểm đối xứng của P qua M và N.
a, Tính AP và diện tích tam giác ABC biết AB = 6cm, AC = 8cm.
b, Chứng minh tứ giác AMPN là hình chữ nhật.
c, Chúng minh tứ giác APCE là hình thoi.
d, Tam giác ABC cần có điều kiện gì để tứ giác APCE là hình vuông?
e, Chứng minh AP, BE, CD đồng quy.
f, Chứng minh ba điểm D, A, E thẳng hàng.
Cho AABC vuông tại A, điểm M là trung điểm của BC. Gọi D và E lần lượt là hình chiếu của M trên AB và AC a) Chứng minh: tứ giác ADME là hình chữ nhật. b) Lấy điểm K đối xứng với M qua D. Tứ giác AEDK là hình gì? Vì sao? c) Chứng minh: tứ giác AMBK là hình thoi. d) Gọi I là điểm đối xứng với M qua E. Chứng minh: K đối xứng với I qua A.
Cho tam giác ABC vuông tại A. Gọi D, E, F lần lượt là trung điểm của AB, BC, AC. a)Chứng minh: Tứ giác ADEF là hình chữ nhật. b)Gọi M là điểm đối xứng của E qua D. Chứng minh: Tứ giác BMAE là hình thôi. c)Cho AB=3cm , BC=5cm. Tính Sabc d)Gọi O là giao điểm của AE và DF. Đường thẳng CO cắt EF tại G. Chứng minh: OG=1:6 CM
Bài 4: Cho tam giác ABC vuông tại A, đường cao AH. Kẻ HE, HF vuông góc với AB, AC lần lượt tại E và F. Gọi M, N, P lần lượt là trung điểm của BC, HB, HC. a) Chứng minh tứ giác AEHF là hình chữ nhật b) Chứng minh EN = 1 2 HB c) C/ minh tứ giác NEFP là hình thăng vuông, tính diện tích của nó biết AB = 6m, AC = 8cm d) Chứng minh AM // EN
Cho tam giác ABC vuông tại A . Gọi M là trung điểm của BC . Vẽ MF⊥ AB ( F thuộc AB ) , ME ⊥ AC ( E thuộc AC )
a, giả sử AC 8cm , AB 6cm. Tính BC và trung tuyến AM
b, chứng minh rằng : tứ giác AEMF là hình chữ nhật
C , gọi điểm N đối xứng với điểm M qua điểm F. Chứng minh tứ giác AMBN là hình thoi
d,gọi I là giao điểm hai đường chéo 2 hình chữ nhật AEMF , đường thẳng BI cắt đường thẳng EM tại điểm K và gọi điểm H là hình chiếu của điểm K xuống đường thẳng NP, chứng minh tam giác AMN cân,
Đọc tiếp
Cho tam giác ABC vuông tại A . Gọi M là trung điểm của BC . Vẽ MF⊥ AB ( F thuộc AB ) , ME ⊥ AC ( E thuộc AC ) a, giả sử AC = 8cm , AB= 6cm. Tính BC và trung tuyến AM b, chứng minh rằng : tứ giác AEMF là hình chữ nhật C , gọi điểm N đối xứng với điểm M qua điểm F. Chứng minh tứ giác AMBN là hình thoi d,gọi I là giao điểm hai đường chéo 2 hình chữ nhật AEMF , đường thẳng BI cắt đường thẳng EM tại điểm K và gọi điểm H là hình chiếu của điểm K xuống đường thẳng NP, chứng minh tam giác AMN cân,
cho tam giác ABC, các điểm M,N,P lần lượt là trung điểm của các cạnh AB, AC, BC, trên tia đối của tia NP lấy điểm D sao cho ND=NP.
a) chứng minh: tứ giác ADCP là hình bình hành
b) gọi F là giao điểm của MN và DC. giả sử MN=3cm. tính BC và chứng minh FD=FC
c) gọi H là giao điểm của AP và MN; I là giao điểm của NP và HC. chứng minh B, I, F thẳng hàng