Chương I: VÉC TƠ
Các câu hỏi tương tự
Đường Tròn (I) Nội Tiếp tam giác ABC, Tiếp Xúc với các cạnh BC, CA, AB lần lượt tại M N P. Chứng minh rằng \(a\overrightarrow{IM}+b\overrightarrow{IN}+c\overrightarrow{IP}=0\)
cho tam giác ABC nội tiếp đường tròn tâm O từ A,B,C kẻ 3 đường phân giác của tam giác lần lượt cắt đường tròn tại A',B',C' . Gọi I là giao điểm của 3 đường phân giác , M là điểm đối xứng của O qua C'B' . Chứng minh vector OM = vector A'I
cho tam giác ABC , có A(-5;6) , trực tâm H(-3;2), M(0;1) là trung điểm BC . tổng hoành đọ và tung đọ của tâm đường tròn ngoai tiếp tam giác abc
A5
B2
C3
D4
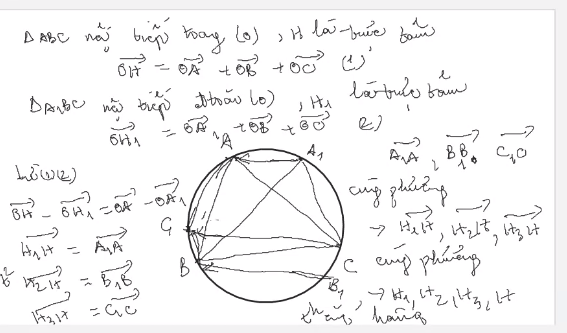
Cho ΔABC đều trọng tâm O. O là tâm đường tròn bán kính R (tùy ý) và chọn 3 điểm A' (≠ A), B'(≠B), C'(≠C) trên đường tròn (O;R) sao cho ΔABC đều và thỏa \(\widehat{AA'O}=\widehat{BB'O}=\widehat{CC'O}\). Chứng minh \(\overrightarrow{AA'}+\overrightarrow{BB'}+\overrightarrow{CC'}=\overrightarrow{0}\)
1)Cho hình bình hành ABCD. Gọi M, N lần lượt là trung điển AB và CD. Đường thẳng AC cắt MD và NB tại R và F. CMR: véc tơ AE=véc tơ EF = véc tơ FC
2) cho đường tròn O và tam giác ABC nội tiếp đường tròn O sao cho BC không đi qua O. Gọi B đối xứng với B qua O, H là trực tâm của tam giác ABC.CMR véc tơ AH ma bằng véc tơ BC
Cho tam giác ABC và hai điểm M,N nằm trên các cạnh AC,AB sao cho MN song song với BC. Điểm P di chuyển trên đoạn thẳng MN. Lấy các điểm E,F sao cho \(EP\perp AC,EC\perp BC,EP\perp AB,FB\perp BC\)
a) Chứng minh rằng đường thẳng EF đi qua một điểm cố định khi P di chuyển
b) Đường thẳng qua A vuông góc với EF cắt BC tại Q. CHứng minh BC đi qua trung điểm PQ
Cho tam giác ABC , gọi M, N lần lượt là trung điểm AB, AC . Trên đường thẳng MN, BC lần lượt lấy điểm E, F sao cho \(\overrightarrow{ME}=-\frac{1}{2}\overrightarrow{NE},\overrightarrow{BF}=\frac{1}{3}\overrightarrow{BC}\) chứng minh 3 đểm A,E,F thẳng hàng
Cho tam giác ABC cân tại A và điểm M bất kì nằm trong tam giác. Qua M kẻ đường thẳng song song với BC cắt AB, AC lần lượt tại D,E. Dựng MK vuông góc với BC tại K gọi I là trung điểm BC. CMR: \(2\overrightarrow{MK}+\overrightarrow{MD}+\overrightarrow{ME}=2\overrightarrow{MI}\)
Cho tam giác ABC có trực tâm H và O là tâm đường tròn ngoại tiếp,G là trọng tâm. Gọi B’ là điểm đối xứng của B qua O . Chứng minh: a) AH =B'C và AB HC ' ,GH=-2 GO