Question

Cho tam giác ABC nhọn, đường cao AK. Vẽ hình chữ nhật CKAD, DB cắt AK tại N. Chứng minh: \(\dfrac{1}{AK^2}=\dfrac{cot^2\widehat{ACB}}{DN^2}+\dfrac{1}{DB^2}\)

Answer 1

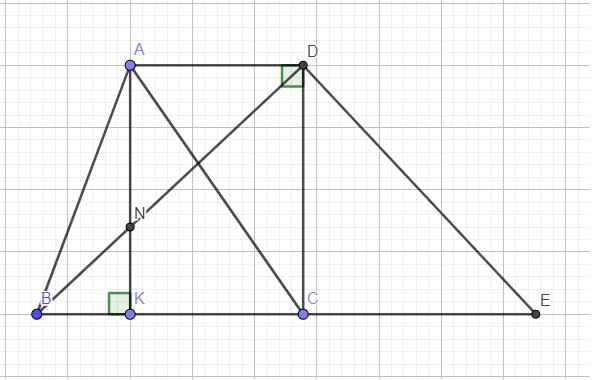
Từ D kẻ đường thẳng vuông góc BD cắt BC kéo dài tại E

Ta có: \(\widehat{ADN}=\widehat{CDE}\) (cùng phụ \(\widehat{NDC}\))

\(\Rightarrow\Delta_vADN\sim\Delta_vCDE\) (g.g)

\(\Rightarrow\dfrac{AD}{CD}=\dfrac{DN}{DE}\Rightarrow\dfrac{1}{DE}=\dfrac{AD}{CD}.\dfrac{1}{DN}=\dfrac{CK}{AK}.\dfrac{1}{DN}=\dfrac{cot\widehat{ACB}}{DN}\)

Áp dụng hệ thức lượng trong tam giác vuông BDE:

\(\dfrac{1}{CD^2}=\dfrac{1}{DE^2}+\dfrac{1}{BD^2}\Leftrightarrow\dfrac{1}{AK^2}=\dfrac{cot^2\widehat{ACB}}{DN^2}+\dfrac{1}{BD^2}\)

Answer 2