Bài 2: Định lý đảo và hệ quả của định lý Talet
Các câu hỏi tương tự
B1 : Cho tam giác ABC, lấy điểm O bất kì trong tam giác đó. Vẽ các tia AO,BO,CO cắt BC,AC,AB lần lượt tại P,Q và R
CM: frac{OA}{AP}+frac{OB}{BQ}+frac{OC}{CR}2
B2: Cho tam giác ABC, vẽ trung tuyến AM. Điểm I bất kì trên AM, F là giao điểm của BI và AC. E là giao điểm của CI và AB. Từ M kẻ đường thẳng song song với IC cắt AB tại H và kẻ đường thẳng song song với IB cắt AC tại K
CM a, EF//HK
b, EF//BC
Các bạn giúp mk nha (Có hình càng tốt)
Đọc tiếp
B1 : Cho tam giác ABC, lấy điểm O bất kì trong tam giác đó. Vẽ các tia AO,BO,CO cắt BC,AC,AB lần lượt tại P,Q và R
CM: \(\frac{OA}{AP}+\frac{OB}{BQ}+\frac{OC}{CR}=2\)
B2: Cho tam giác ABC, vẽ trung tuyến AM. Điểm I bất kì trên AM, F là giao điểm của BI và AC. E là giao điểm của CI và AB. Từ M kẻ đường thẳng song song với IC cắt AB tại H và kẻ đường thẳng song song với IB cắt AC tại K
CM a, EF\(//\)HK
b, EF\(//\)BC
Các bạn giúp mk nha (Có hình càng tốt)
Cho tam giác ABC . E là trung điểm AB. Trên nửa mặt phẳng bờ BC có chứa A vẽ tia Cx song song AB, qua E vé đường thẳng song song với BC cắt AC tại D và cắt Cx tại F, BF cắt AC tại I.
Chứng minh \(\frac{1}{IC}\)=\(\frac{1}{CD}\)+\(\frac{1}{CA}\)Cho tam giác ABC, lấy điểm M thuộc BC và N thuộc AM. Gọi I,K lần lượt là trung điểm của BN và CN. Tia MI cắt AB tại E, tia MK cắt AC tại F. Chứng minh EF song song BC
Cho tam giác ABC .Lấy M là điểm tùy ý trên BC .Qua qua B và C và các đường thẳng song song với AB cắt đường thẳng AC và AB lần lượt tại N và P .Xác định vị trí điểm M để \(\frac{1}{BN}+\frac{1}{CD}\) đạt GTLN
cho TAM GIÁC abcd có am là trung tuyến và điểm e thuộc đoạn thẳng mc. qua e kẻ đường thẳng song song với ac, cắt ab ở d và cắt am ở k. qua e kẻ đường thảng song song với ab, cắt ac ở f. chứng minh cf=dk
Cho tam giác ABC và trung tuyến AM. Điểm O bất kì thuộc AM, F là giao điểm của BO và AC, E là giao điểm của CO và AB. Từ M kẻ đường thẳng song song với OC cắt AB tại H và kẻ đường thẳng song song với OB cắt OC tại K
cho tam giác ABC có AM là đường trung tuyến, I thuộc AM, BI cắt AC tại E, CI cắt AB tại F. Chứng minh FE song song BC( gợi í: đường thẳng A song song BC)
Có ai giải hộ vớiCho hình thang ABCD (AB //CD). Đường thẳng song song với đáy AB cắt các cạnh bên và các đường chéo AD, BD, AC và BC theo thứ tự tại các điểm M, N, P, Q chứng minh 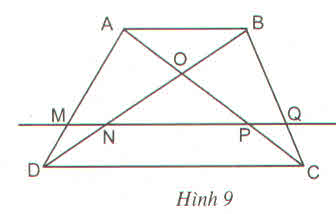 DN\BD=CP\AC
DN\BD=CP\AC









