Question

Cho tam giác \(ABC\) có đường trung tuyến \(AM\). Đường phân giác của góc \(AMB\) cắt \(AB\) tại \(D\) và đường phần giác góc \(AMC\) cắt \(AC\) tại \(E\) (Hình 8). Chứng minh \(DE//BC\).

Answer 1

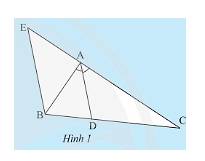
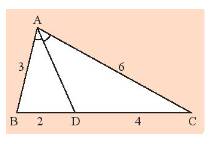
Vì \(MD\) là tia phân giác của góc \(\widehat {AMB}\) nên \(\frac{{AD}}{{DB}} = \frac{{AM}}{{BM}}\) (1)

Vì \(ME\) là tia phân giác của góc \(\widehat {AMC}\) nên \(\frac{{AE}}{{EC}} = \frac{{AM}}{{MC}}\)(2);

Mà \(M\) là trung điểm của \(BC\) nên \(BM = MC\) (3)

Từ (1); (2); (3) \( \Rightarrow \frac{{AD}}{{BD}} = \frac{{AE}}{{EC}}\)

Xét tam giác \(ABC\) có: \(\frac{{AD}}{{BD}} = \frac{{AE}}{{EC}}\)

Do đó, \(DE//BC\)(Định lí Thales đảo).

Answer 2

Xét ΔMAB có MD là phân giác

nên AD/DB=AM/MB=AM/MC

Xét ΔAMC có ME là phân giác

nên AE/EC=AM/MC

=>AD/DB=AE/EC

=>DE//BC