Đường phân giác \(AD\) của tam giác \(ABC\) chia cạnh đối diện \(BC\) thành hai đoạn thẳng tỉ lệ với hai đoạn thẳng nào trong hình?
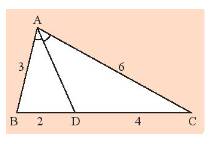
Đường phân giác \(AD\) của tam giác \(ABC\) chia cạnh đối diện \(BC\) thành hai đoạn thẳng tỉ lệ với hai đoạn thẳng nào trong hình?

Cho tam giác \(ABC\) có đường phân giác \(AD\). Vẽ đường thẳng qua \(B\) song song với \(AD\) và cẳ đường thẳng \(AC\) tại \(E\) (Hình 1). Hãy giảu thích tại sao:
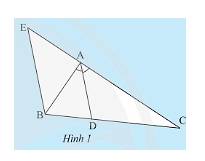
a) Tam giác \(BAE\) cân tại \(A\).
b) \(\frac{{DB}}{{DC}} = \frac{{AE}}{{AC}} = \frac{{AB}}{{AC}}\).
Thảo luận (2)Hướng dẫn giảia) Vì \(BE//AD\) nên \(\widehat {EBA} = \widehat {BAD}\) (cặp góc so le trong) (1)
Vì \(BE//AD\) nên \(\widehat {BEA} = \widehat {DAC}\) (cặp góc đồng vị) (2)
Vì \(AD\) là tia phân giác nên \(\widehat {BAD} = \widehat {DAC}\) (tính chất) (3)
Từ (1); (2); (3) suy ra \(\widehat {EBA} = \widehat {AEB}\) (tính chất bắc cầu)
Xét tam giác \(BAE\) có:
\(\widehat {EBA} = \widehat {AEB}\) (chứng minh trên)
Nên tam giác \(BAE\) cân tại \(A\).
b) Vì \(BE//AD\) nên \(\frac{{BD}}{{DC}} = \frac{{AE}}{{AC}}\).
Mà tam giác \(BAE\) cân tại \(A\) nên \(AE = AB \Rightarrow \frac{{AE}}{{AC}} = \frac{{AB}}{{AC}}\) (định lí Thales)
Do đó, \(\frac{{DB}}{{DC}} = \frac{{AE}}{{AC}} = \frac{{AB}}{{AC}}\) (điều phải chứng minh).
(Trả lời bởi Hà Quang Minh)
Tính độ dài cạnh \(MQ\) của tam giác \(MPQ\) trong Hình 6.

Thảo luận (1)Hướng dẫn giảiVì \(MN\) là phân giác của góc \(PMQ\) nên theo tính chất đường phân giác ta có:
\(\frac{{PN}}{{QN}} = \frac{{MP}}{{MQ}} \Leftrightarrow \frac{4}{5} = \frac{7}{{MQ}} \Rightarrow MQ = \frac{{5.7}}{4} = \frac{{35}}{4}\).
Vậy \(MQ = \frac{{35}}{4}\)
(Trả lời bởi Hà Quang Minh)
Tính độ dài \(x\) trong Hình 7.

Thảo luận (2)Hướng dẫn giảia) Vì \(AD\) là phân giác của góc \(BAC\) nên theo tính chất đường phân giác ta có:
\(\frac{{CD}}{{BD}} = \frac{{AC}}{{AB}} \Leftrightarrow \frac{x}{{2,4}} = \frac{5}{3} \Rightarrow x = \frac{{2,4.5}}{3} = 4\).
Vậy \(x = 4\).
b) Ta có: \(GH + HF = GF \Rightarrow HF = GF - GH = 20 - x\)
Vì \(EH\) là phân giác của góc \(GEF\) nên theo tính chất đường phân giác ta có:
\(\frac{{GH}}{{HF}} = \frac{{GE}}{{EF}} \Leftrightarrow \frac{x}{{20 - x}} = \frac{{18}}{{12}} \Leftrightarrow \frac{x}{{20 - x}} = \frac{3}{2} \Rightarrow 2x = 3.\left( {20 - x} \right)\)
\( \Leftrightarrow 2x = 60 - 3x \Leftrightarrow 5x = 60 \Rightarrow x = 12\)
Vậy \(x = 12\).
c) Vì \(RS\) là phân giác của góc \(RPQ\) nên theo tính chất đường phân giác ta có:
\(\frac{{PS}}{{SQ}} = \frac{{PR}}{{RQ}} \Leftrightarrow \frac{5}{6} = \frac{{10}}{x} \Rightarrow x = \frac{{10.6}}{5} = 12\).
Vậy \(x = 12\).
(Trả lời bởi Hà Quang Minh)
Tam giác \(ABC\) có \(AB = 6cm,AC = 8cm,BC = 10cm\). Đường phân giác của góc \(BAC\) cắt cạnh \(BC\) tại \(D\).
a) Tính độ dài các đoạn thẳng \(DB\) và \(DC\).
b) Tính tỉ số diện tích giữa \(\Delta ADB\) và \(\Delta ADC\).
Thảo luận (1)Hướng dẫn giải
a) Ta có: \(BD + DC = BC \Rightarrow DC = BC - BD = 10 - BD\)
Vì \(AD\) là phân giác của góc \(BAC\) nên theo tính chất đường phân giác ta có:
\(\frac{{BD}}{{DC}} = \frac{{AB}}{{AC}} \Leftrightarrow \frac{{BD}}{{10 - BD}} = \frac{6}{8} \Leftrightarrow 8BD = 6.\left( {10 - BD} \right) \Rightarrow 8BD = 60 - 6BD\)
\( \Leftrightarrow 8BD + 6BD = 60 \Leftrightarrow 14BD = 60 \Rightarrow BD = \frac{{60}}{{14}} = \frac{{30}}{7}\)
\( \Rightarrow DC = 10 - \frac{{30}}{7} = \frac{{40}}{7}\)
Vậy \(BD = \frac{{30}}{7}cm;DC = \frac{{40}}{7}cm\).
b) Kẻ \(AE \bot BC \Rightarrow AE\) là đường cao của tam giác \(ABC\).
Vì \(AE \bot BC \Rightarrow AE \bot BD \Rightarrow AE\)là đường cao của tam giác \(ADB\)
Diện tích tam giác \(ADB\) là:
\({S_{ADB}} = \frac{1}{2}BD.AE\)
Vì \(AE \bot BC \Rightarrow AE \bot DC \Rightarrow AE\)là đường cao của tam giác \(ADC\)
Diện tích tam giác \(ADC\) là:
\({S_{ADC}} = \frac{1}{2}DC.AE\)
Ta có: \(\frac{{{S_{ADB}}}}{{{S_{ADC}}}} = \frac{{\frac{1}{2}AE.BD}}{{\frac{1}{2}AE.CD}} = \frac{{BD}}{{DC}} = \frac{{\frac{{30}}{7}}}{{\frac{{40}}{7}}} = \frac{3}{4}\).
Vậy tỉ số diện tích giữa \(\Delta ADB\) và \(\Delta ADC\) là \(\frac{3}{4}\).
(Trả lời bởi Kiều Sơn Tùng)
Tam giác \(ABC\) có \(AB = 15cm,AC = 20cm,BC = 25cm\). Đường phân giác của góc \(BAC\)cắt \(BC\) tại \(D\). Qua \(D\) vẽ \(DE//AB\left( {E \in AC} \right)\).
a) Tính độ dài các đoạn thẳng \(BD,DC\) và \(DE\).
b) Chứng minh \(ABC\) là tam giác vuông. Tính diện tích tam giác \(ABC\).
c) Tính diện tích tam giác \(ADB,ADE\) và \(DCE\).
Thảo luận (2)Hướng dẫn giảia) Ta có: \(BD + DC = BC \Rightarrow DC = BC - BD = 25 - BD\)
Vì \(AD\) là phân giác của góc \(BAC\) nên theo tính chất đường phân giác ta có:
\(\frac{{BD}}{{DC}} = \frac{{AB}}{{AC}} \Leftrightarrow \frac{{BD}}{{25 - BD}} = \frac{{15}}{{20}} \Leftrightarrow 20.BD = 15.\left( {25 - BD} \right) \Rightarrow 20.BD = 375 - 15.BD\)
\( \Leftrightarrow 20BD + 15BD = 375 \Leftrightarrow 35BD = 375 \Rightarrow BD = \frac{{375}}{{35}} = \frac{{75}}{7}\)
\( \Rightarrow DC = 25 - \frac{{75}}{7} = \frac{{100}}{7}\)
Vậy \(BD = \frac{{75}}{7}cm;DC = \frac{{100}}{7}cm\).
Vì \(DE//AB\) nên \(\frac{{DC}}{{BC}} = \frac{{DE}}{{AB}} \Rightarrow \frac{{\frac{{100}}{7}}}{{25}} = \frac{{DE}}{{15}} \Leftrightarrow DE = \frac{{100}}{7}.15:25 = \frac{{60}}{7}\) (hệ quả của định lí Thales).
Vậy \(BD = \frac{{75}}{7}cm;DC = \frac{{100}}{7}cm;DE = \frac{{60}}{7}cm\).
b) Xét tam giác \(ABC\) có:
\(B{C^2} = {25^2} = 625;A{C^2} = {20^2} = 400;A{B^2} = {15^2} = 225\)
\( \Rightarrow B{C^2} = A{C^2} + A{B^2}\)
Do đó, tam giác\(ABC\) là tam giác vuông tại \(A\).
c) Diện tích tam giác \(ABC\) là
\({S_{ABC}} = \frac{1}{2}AB.AC = \frac{1}{2}.15.20 = 150\left( {c{m^2}} \right)\).
Xét tam giác \(ADB\) và tam giác \(ABC\) ta có:
\(\frac{{BD}}{{BC}} = \frac{{\frac{{75}}{7}}}{{25}} = \frac{3}{7}\) và có chung chiều cao hạ từ đỉnh \(A\). Do đó, diện tích tam giác \(ADB\) bằng \(\frac{3}{7}\) diện tích tam giác \(ABC\).
Diện tích tam giác \(ADB\) là:
\({S_{ADB}} = 150.\frac{3}{7} = \frac{{450}}{7}\left( {c{m^2}} \right)\).
Diện tích tam giác \(ACD\) là:
\({S_{ACD}} = {S_{ABC}} - {S_{ADB}} = 150 - \frac{{450}}{7} = \frac{{600}}{7}\)
Vì \(ED//AB \Rightarrow \frac{{CE}}{{AE}} = \frac{{CD}}{{BD}} = \frac{{\frac{{100}}{7}}}{{\frac{{75}}{{100}}}} = \frac{4}{3}\)
Xét tam giác \(ADE\) và tam giác \(DCE\) ta có:
\(\frac{{CE}}{{AE}} = \frac{4}{3}\) và hai tam giác này có chung đường cao hạ từ \(D\).
Do đó, \(\frac{{{S_{ADE}}}}{{{S_{DCE}}}} = \frac{4}{3}\).
Diện tích tam giác \(ADE\) là
\({S_{ADE}} = \frac{{600}}{7}:\left( {3 + 4} \right).4 = \frac{{2400}}{{49}}\left( {c{m^2}} \right)\)
\({S_{DCE}} = \frac{{600}}{7}:\left( {3 + 4} \right).3 = \frac{{1800}}{{49}}\left( {c{m^2}} \right)\).
(Trả lời bởi Kiều Sơn Tùng)
Cho tam giác \(ABC\) vuông tại \(A\) có \(AB = 3cm,AC = 4cm.\) Đường phân giác của góc \(A\) cắt \(BC\) tại \(D\).
a) Tính \(BC,BD,DC\).
b) Vẽ đường cao \(AH\). Tính \(AH,HD\) và \(AD\).
Thảo luận (1)Hướng dẫn giải
a)
Xét tam giác \(ABC\) vuông tại \(A\) ta có:
\(A{B^2} + A{C^2} = B{C^2}\)
\( \Leftrightarrow {3^2} + {4^2} = B{C^2}\)
\( \Leftrightarrow B{C^2} = 25\)
\( \Rightarrow BC = 5cm\)
Ta có: \(BD + DC = BC \Rightarrow DC = BC - BD = 5 - BD\)
Vì \(AD\) là phân giác của góc \(BAC\) nên theo tính chất đường phân giác ta có:
\(\frac{{BD}}{{DC}} = \frac{{AB}}{{AC}} \Leftrightarrow \frac{{BD}}{{5 - BD}} = \frac{3}{4} \Leftrightarrow 4.BD = 3.\left( {5 - BD} \right) \Rightarrow 4.BD = 15 - 3.BD\)
\( \Leftrightarrow 4BD + 3BD = 15 \Leftrightarrow 7BD = 15 \Rightarrow BD = \frac{{15}}{7}\)
\( \Rightarrow DC = 5 - \frac{{15}}{7} = \frac{{20}}{7}\)
Vậy \(BC = 5cm;BD = \frac{{15}}{7}cm;DC = \frac{{20}}{7}cm\).
b) Diện tích tam giác \(ABC\) vuông tại \(A\) là:
\({S_{ABC}} = \frac{1}{2}AB.AC = \frac{1}{2}.4.3 = 6\left( {c{m^2}} \right)\)
Mặt khác \({S_{ABC}} = \frac{1}{2}.AH.BC = \frac{1}{2}.AH.5 = 6\)
\( \Rightarrow AH = \frac{{6.2}}{5} = 2,4cm\).
Xét tam giác \(AHB\) vuông tại \(H\) ta có:
\(A{H^2} + H{B^2} = A{B^2}\)
\( \Leftrightarrow H{B^2} = A{B^2} - A{H^2}\)
\( \Leftrightarrow H{B^2} = {3^2} - 2,{4^2}\)
\( \Leftrightarrow H{B^2} = 3,24\)
\( \Rightarrow HB = 1,8cm\)
\(HD = BD - BH = \frac{{15}}{7} - 1,8 = \frac{{12}}{7}cm\).
Xét tam giác \(AHD\) vuông tại \(H\) ta có:
\(A{H^2} + H{D^2} = A{D^2}\)
\( \Leftrightarrow A{D^2} = {\left( {\frac{{12}}{7}} \right)^2} + 2,{4^2}\)
\( \Leftrightarrow A{D^2} = \frac{{144}}{{49}} + \frac{{144}}{{25}}\)
\( \Rightarrow AD \approx 2,95cm\)
Vậy \(AH = 2,4cm;HD = \frac{{12}}{7}cm;AD = 2,95cm\).
(Trả lời bởi Kiều Sơn Tùng)
Cho tam giác \(ABC\) có đường trung tuyến \(AM\). Đường phân giác của góc \(AMB\) cắt \(AB\) tại \(D\) và đường phần giác góc \(AMC\) cắt \(AC\) tại \(E\) (Hình 8). Chứng minh \(DE//BC\).
Thảo luận (2)Hướng dẫn giảiVì \(MD\) là tia phân giác của góc \(\widehat {AMB}\) nên \(\frac{{AD}}{{DB}} = \frac{{AM}}{{BM}}\) (1)
Vì \(ME\) là tia phân giác của góc \(\widehat {AMC}\) nên \(\frac{{AE}}{{EC}} = \frac{{AM}}{{MC}}\)(2);
Mà \(M\) là trung điểm của \(BC\) nên \(BM = MC\) (3)
Từ (1); (2); (3) \( \Rightarrow \frac{{AD}}{{BD}} = \frac{{AE}}{{EC}}\)
Xét tam giác \(ABC\) có: \(\frac{{AD}}{{BD}} = \frac{{AE}}{{EC}}\)
Do đó, \(DE//BC\)(Định lí Thales đảo).
(Trả lời bởi Hà Quang Minh)