Lời giải:
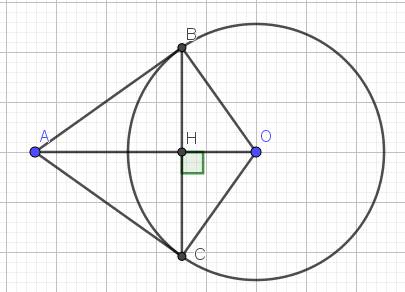
a. Vì $AB$ là tiếp tuyến của $(O)$ nên $AB\perp BO$. Tức là tam giác $ABO$ vuông tại $B$
$AB=\sqrt{OA^2-OB^2}=\sqrt{5^2-3^2}=4$ (cm)
$\frac{AB}{OA}=\sin \widehat{O_1}=\frac{BH}{BO}$
$\Rightarrow BH=\frac{AB.BO}{OA}=\frac{4.3}{5}=\frac{12}{5}$ (cm)
c.
Vì $BOC$ là tam giác cân tại $O$ (OB=OC=R) nên đường cao $OH$ đồng thời là đường trung trực của $BC$
$A,H,O$ thẳng hàng nên $A$ cũng nằm trên đường trung trực của $BC$
$\Rightarrow AB=AC$
Xét tam giác $ABO$ và $ACO$ có:
$AB=AC$
$BO=CO$
$AO$ chung
$\Rightarrow \triangle ABO=\triangle ACO$ (c.c.c)
$\Rightarrow \widehat{ACO}=\widehat{ABO}=90^0$
$\Rightarrow AC$ là tiếp tuyến của $(O)$
b.
Vì $\triangle ABO=\triangle ACO$ nên $\widehat{BAO}=\widehat{CAO}$
$\Rightarrow \widehat{BAC}=2\widehat{BAO}$
$\sin \widehat{BAO}=\frac{BO}{AO}=\frac{3}{5}$
$\Rightarrow \widehat{BAO}=37^0$
$\Rightarrow \widehat{BAC}=2\widehat{BAO}=2.37^0=74^0$