Chương 1:ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
Các câu hỏi tương tự
Xét tính đồng biến, nghịch biến của hàm số và tìm cực trị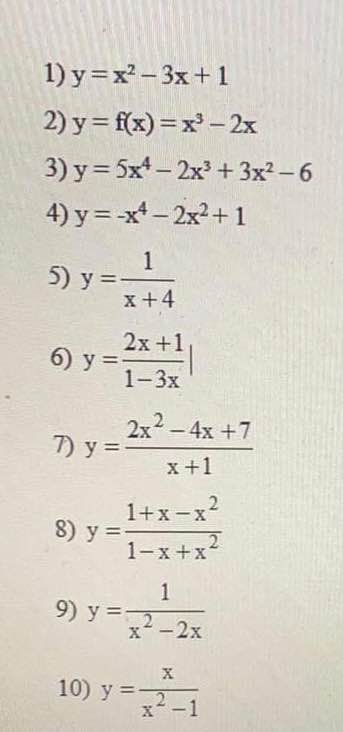
Câu 4. Cho hàm số \(y = x^4 - 2x^2 -3\). Mệnh đề nào sau đây là mệnh đề đúng?
A. Hàm số nghịch biến trên \((-1; 0).\)
B. Hàm số đồng biến trên \((-\infty;0).\)
C. Hàm số nghịch biến trên \((-1; 1).\)
D. Hàm số nghịch biến trên \((0; +\infty).\)
Tìm tất cả các giá trị thực của m để hàm số y = mx+6/2x+m+1 nghịch biến trên khoảng (-1;1)
tìm m để đồ thị hàm số \(\left(C_m\right):y=x^3-3mx^2+3\left(m^2-1\right)x-m^3+m\) có cực trị đồng thời khoảng cách từ điểm cực đại của đồ thị hàm số O bằng √2 lần khoảng cách từ điểm cực tiểu của đồ thị hàm số đến O ( O là gốc tọa độ )
tìm m để đồ thị hàm số \(\left(C_m\right):y=x^3-3mx^2+3\left(m^2-1\right)x-m^3+m\) có cực trị đồng thời khoảng cách từ điểm cực đại của đồ thị hàm số O bằng \(\sqrt{2}\) lần khoảng cách từ điểm cực tiểu của đồ thị hàm số đến O ( O là gốc tọa độ )
tìm m để hàm số \(=-x^4+\left(2m-3\right)x^2+m\) nghịch biến trên (1;3)
tìm m để hàm số \(y=\dfrac{x^3}{3}-\dfrac{mx^2}{2}+2mx-3m+4\) nghịch biến trên một đoạn có độ dài bằng 3.
tìm m để hàm số \(y=x^3+3x^2+\left(m+1\right)x+4m\) nghịch biến trên (-1;1)
tìm m để hàm số \(y=x^4-2\left(m-1\right)x^2+m-2\) đồng biến trên (1;3)
(theo 2 cách )






