nè
Khi Rb= 3 ⇒ P1 = \(\dfrac{U^2.R_b}{\left(R_0+R_b\right)^2}=\dfrac{U^2.3}{\left(R_0+3\right)^2}\)
Khi Rb= 12 ⇒ P2 = \(\dfrac{U^2.12}{\left(R_0+12\right)^2}\)
ta có P1= P2 =a ⇒ \(\dfrac{3}{\left(R_0+3\right)^2}=\dfrac{12}{\left(R_0+12\right)^2}\)
⇔ 4(R0 + 3)2 = (R0 + 12)2
⇔ 4R20 + 24R0 + 36 = R20 + 24R0 + 144
⇔ 3R20 = 108
⇔ R0 = 6Ω
Ta có P1=a ⇔\(\dfrac{U^2.3}{\left(6+3\right)^2}=a\Rightarrow3.U^2=81a\)
⇔ U2= 27a
Ta có Pb= \(\dfrac{U^2R_b}{\left(6+R_b\right)^2}=\dfrac{729a}{\dfrac{6^2}{R_b}+R_b+12}\)
Áp dụng BĐT Cauchy
⇒ \(\dfrac{6^2}{R_b}+R_b\ge2\sqrt{\dfrac{6^2}{R_b}.R_b}=12\)
Dấu "=" xảy ra ⇔ Rb = 6Ω
⇒ Pb ≤ \(\dfrac{729a}{12+12}=30,375a\)
Vậy Pbmax=30,375a ⇔ Rb=6Ω
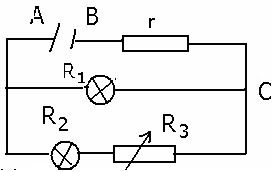sao r nt (r1//r2) vậy? mình thấy nó song song hết mà
