Sửa đề: Cho ΔMNP vuông tại M, đường cao MK. Em hãy viết các hệ thức lượng đã học
Xét ΔMNP vuông tại M có MK là đường cao
nên \(NK\cdot NP=NM^2;PK\cdot PN=PM^2\)
\(\frac{1}{MK^2}=\frac{1}{MN^2}+\frac{1}{MP^2}\)
\(MK^2=KN\cdot KP\)
\(MN^2+MP^2=NP^2\)
Sửa đề: Cho ΔMNP vuông tại M, đường cao MK. Em hãy viết các hệ thức lượng đã học
Xét ΔMNP vuông tại M có MK là đường cao
nên \(NK\cdot NP=NM^2;PK\cdot PN=PM^2\)
\(\frac{1}{MK^2}=\frac{1}{MN^2}+\frac{1}{MP^2}\)
\(MK^2=KN\cdot KP\)
\(MN^2+MP^2=NP^2\)
cho hình vẽ sau , viết công thức tính độ dài các cạnh trong tam giác ABC vuông tại A, đường cao AH
Cho hình 36.
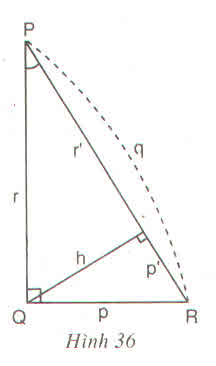
Hãy viết hệ thức giữa :
a) Cạnh huyền, cạnh góc vuông và hình chiếu của nó trên cạnh huyền
b) Các cạnh góc vuong p, r và đường cao h
c) Đường cao h và hình chiếu của các cạnh góc vuông trên cạnh huyền p', r'
cho tam giác vuông abc vuông tại A, đường cao ah, hệ thức nào sau đây là đúng:
cosC= ab/ac
tanB=ab/ac
cotC=hc/ha
cotB=ac/ab
Cho biểu thức: A=15cân4a+cân a-cân25a a) rút gọn A b) tính giá trị của biểu thức A tại A=100 b) Vẽ AM là đường trung tuyến của tam giác ABC (M thuộc BC) . Chứng minh góc BAH= góc MAC c) Vẻ HE vuông góc AB (E thuộc AB), HF vuông góc AC (F thuộc AC) . Chứng minh EF vuông góc AM tại K và tính độ dài AK
Cho ∆KMP vuông tại K , biết Góc P = 30° ; KP = 8cm. Các đường cao KH và HE ( H € MP ; E € KM ) a/ Cho Hình vẽ b/ Tính : KH ; KM ; MP ; EK b/ HE² = EK. EM
cho tam giác ABC vuông tại A, có độ dài của các cạnh thỏa mãn hệ thức: BC^2 = (căn 3 + 1)AC^2 + ( căn 3 - 1 ) AB.AC. Tính số đo góc ABC
Cho tam giác MNP vuông tại M (MN-MP), đường cao MH. Gọi D và E lần lượt là hình chiếu của H trên MN và MP. 2/ Chứng minh: MD.MN =ME, MP MN² b/ Chứng minh: MP4 PH và chứng minh MH = NPNDPE NH có Qua M kẻ đường vuông góc với DE cắt NP tại K. Chứng minh Kỉ là trung điểm Nh d/ Cho góc P=a; NP = a. Từ M kẻ đường vuông góc với MK cắt tia PN tại I. Chứng minh PI a.(cos 2a+1) 2cos 2a
Cho tam giác ABC vuông tại A, đường cao AH. Gọi E, F lần lượt là hình chiếu của H trên AB, AC
a, Cho AB=9, BH=5.4. Tính AC,BC,AH,EF ( đã làm được)
b, Chứng minh \(\dfrac{1}{EF^2}\)=\(\dfrac{1}{AB^2}\)+\(\dfrac{1}{AC^2}\)(đã làm được)
c, Chứng minh EA.EB+FA.FC=HB.HC( cần trợ giúp)
Cho tam giác ABC vuông tại A, đường cao AH chia cạnh huyền BC thành hai đoạn BH, CH có độ dài lần lượt là 4cm, 9cm. Gọi D và E lần lượt là hình chiếu của H trên AB và AC
a) Tính độ dài đoạn thẳng DE
b) Các đường thẳng vuông góc với DE tại D và tại E lần lượt cắt BC tại M và N. Chứng minh M là trung điểm của BH và N là trung điểm của CH
c) Tính diện tích tứ giác DENM