a . \(\left(SAC\right)\cap\left(SBC\right)=SC\) (3)
Trên (SAC) hạ \(AH\perp SC\left(2\right)\) ; trên \(\left(SAB\right)\) hạ \(AK\perp SB\)
C/m : HK \(\perp SC\) <- \(SC\perp\left(AHK\right)\) <- \(AK\perp SC\)
C/m : AK \(\perp SC\) . Ta có : \(BC\perp\left(SAB\right)\Rightarrow\left(SBC\right)\perp\left(SBA\right)\Rightarrow AK\perp\left(SBC\right)\left(AK\perp SB\right)\)
\(\Rightarrow AK\perp SC\) . Từ đó ; c/m được : \(HK\perp SC\) (1)
Từ (1) ; (2) ; (3) suy ra : \(\left(\left(SAC\right);\left(SBC\right)\right)=\widehat{AHK}\)
Tính được : AH ; AK ; mặt khác : \(AK\perp\left(SBC\right)\Rightarrow AK\perp HK\)
\(\Rightarrow\) \(\Delta HKA\) \(\perp\) tại K
\(\Rightarrow...\)
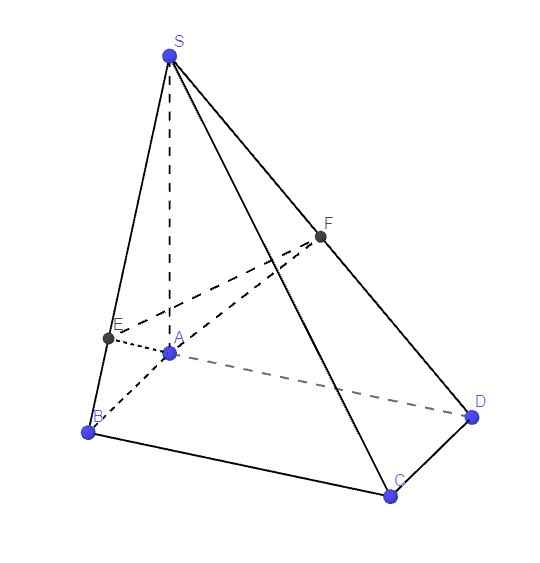
b. Từ A kẻ \(AE\perp SB\) ; \(AF\perp SD\)
Dễ dàng chứng minh \(AE\perp\left(SBC\right)\) và \(AF\perp\left(SCD\right)\)
\(\Rightarrow\) Góc giữa (SBC) và (SCD) là góc giữa AE và AF (là góc \(\widehat{EAF}\) nếu nó nhọn và là góc bù với \(\widehat{EAF}\) nếu nó tù)
Hệ thức lượng: \(AE=\dfrac{SA.AB}{\sqrt{SA^2+AB^2}}=\dfrac{a\sqrt{3}}{2}\) ; \(SE=\sqrt{SA^2-AE^2}=\dfrac{3a}{2}\)
\(AF=\dfrac{SA.AD}{\sqrt{SA^2+AD^2}}=\dfrac{a\sqrt{6}}{2}\) ; \(SF=\sqrt{SA^2-AF^2}=\dfrac{a\sqrt{6}}{2}\)
Áp dụng định lý hàm cos trong tam giác SBD:
\(cos\widehat{BSD}=\dfrac{SB^2+SD^2-BD^2}{2SB.SD}=\dfrac{\sqrt{6}}{4}\)
Áp dụng định lý hàm cos trong tam giác SEF:
\(EF=\sqrt{SE^2+SF^2-2SE.SF.cos\widehat{BSD}}=\dfrac{a\sqrt{6}}{2}\)
\(\Rightarrow cos\widehat{EAF}=\dfrac{AE^2+AF^2-EF^2}{2AE.AF}=\dfrac{\sqrt{2}}{4}\)
\(\Rightarrow\widehat{EAF}\approx69^018'\)