Question

cho hình chóp SABC đáy là tam giác vuông cân tại B, AC=2a, SA vuông góc với đáy, SA=a, M là trung điểm của AC

a.cm BM vuông góc (SAC)

b.cm SBC là tam giác vuông

c. gọi (\(\alpha\)) là mặt phẳng đi qua B và vuông góc với SC. xác định thiết diện và tính diện tích

Answer 1

      

Answer 2

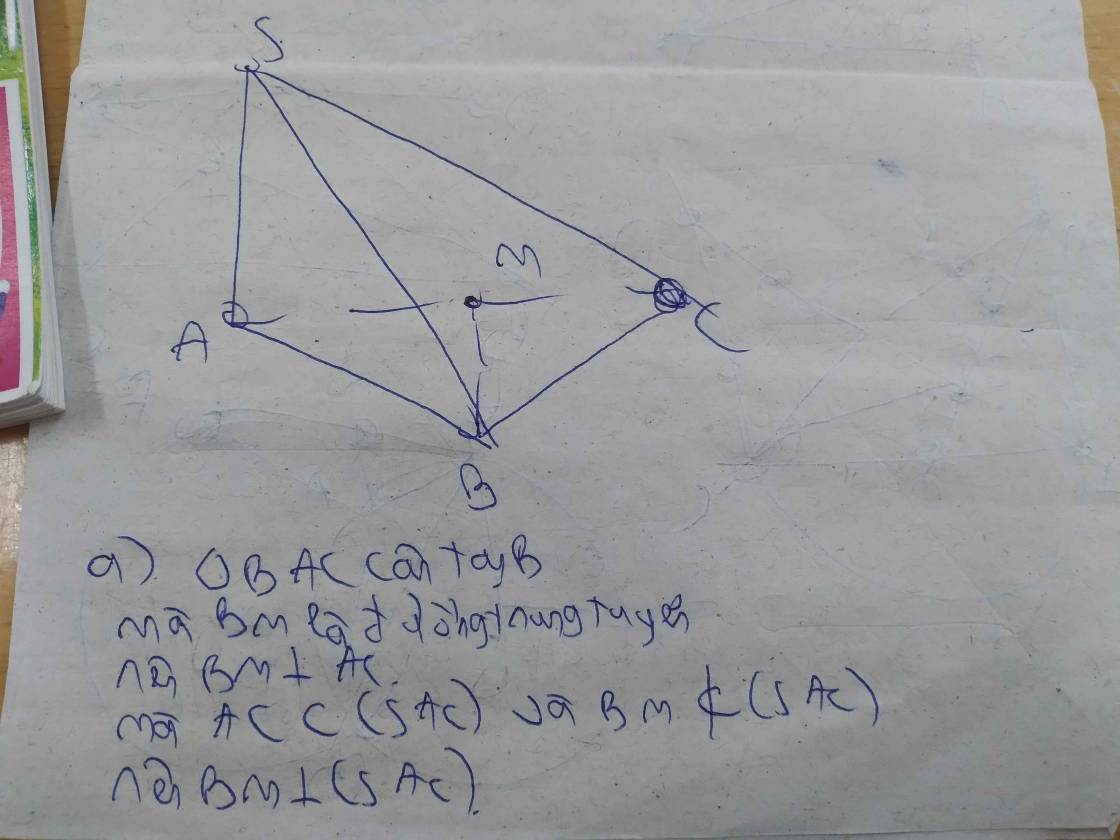
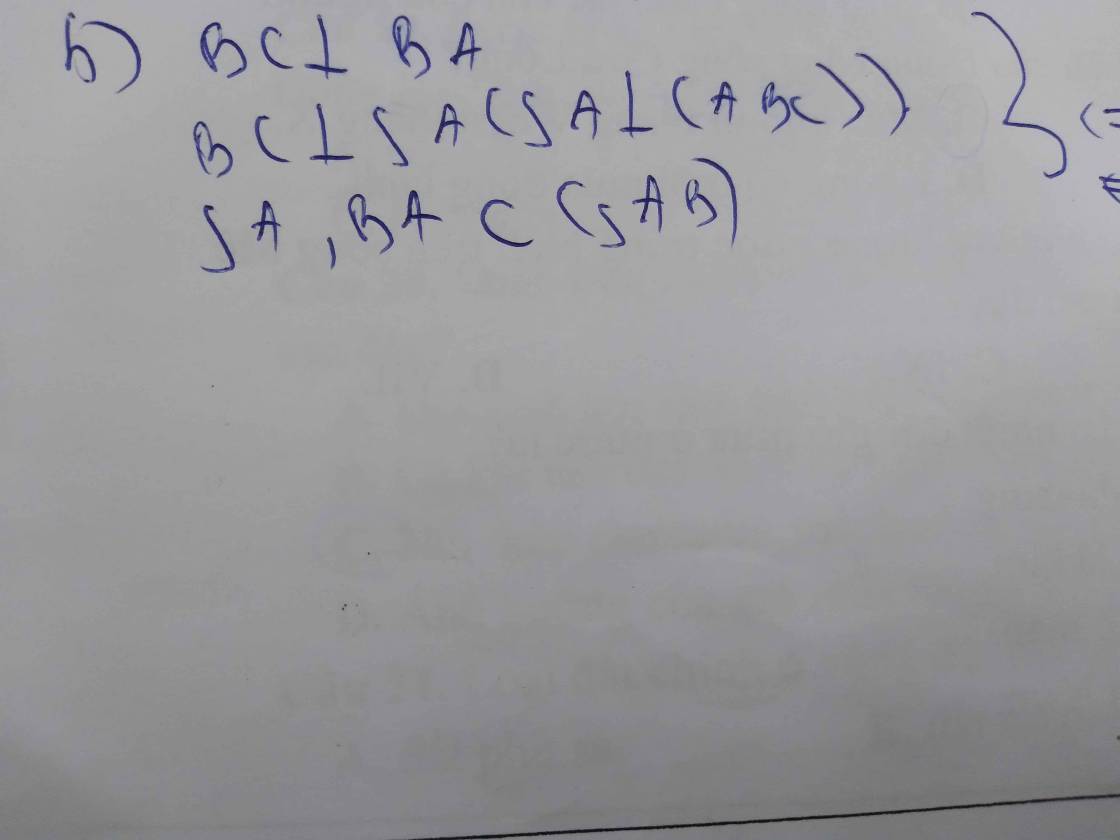c.

Từ M kẻ \(MH\perp SC\) (H thuộc SC)

\(\Rightarrow H\in\left(\alpha\right)\Rightarrow\) thiết diện là tam giác BMH

Do \(\left\{{}\begin{matrix}BM\perp\left(SAC\right)\\MH\in\left(SAC\right)\end{matrix}\right.\) \(\Rightarrow BM\perp MH\Rightarrow\Delta BMH\) vuông tại M

Trong tam giác vuông ABC: \(BM=\dfrac{1}{2}AC=a\) (trung tuyến ứng với cạnh huyền)

Hai tam giác vuông CHM và CAS đồng dạng (chung góc C)

\(\Rightarrow\dfrac{MH}{SA}=\dfrac{CM}{SC}\Rightarrow MH=\dfrac{SA.CM}{SC}=\dfrac{SA.\dfrac{AC}{2}}{\sqrt{SA^2+AC^2}}=\dfrac{a\sqrt{5}}{5}\)

\(\Rightarrow S_{BMH}=\dfrac{1}{2}BM.MH=\dfrac{a^2\sqrt{5}}{10}\)