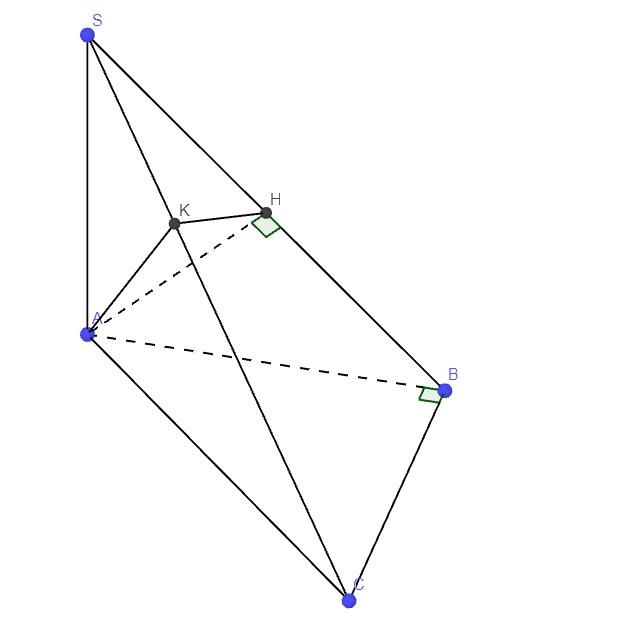
a.
\(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\AB\perp BC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
\(\Rightarrow BC\perp AH\)
Mà \(AH\perp SB\left(gt\right)\)
\(\Rightarrow AH\perp\left(SBC\right)\)
b.
Từ H kẻ \(HK\perp SC\) (K thuộc SC) (1)
Do \(AH\perp\left(SBC\right)\Rightarrow AH\perp SC\) (2)
\(\left(1\right);\left(2\right)\Rightarrow SC\perp\left(AHK\right)\)
Mà \(SC=\left(SAC\right)\cap\left(SBC\right)\)
\(\Rightarrow\widehat{AKH}\) là góc giữa (SAC) và (SBC)
\(SC\perp\left(AHK\right)\Rightarrow SC\perp AK\)
\(AC=AB\sqrt{2}=a\sqrt{2}\)
Áp dụng hệ thức lượng trong tam giác vuông SAC:
\(AK=\dfrac{SA.AC}{\sqrt{SA^2+AC^2}}=\dfrac{a\sqrt{6}}{3}\)
Hệ thức lượng trong tam giác vuông SAB:
\(AH=\dfrac{SA.AB}{\sqrt{SA^2+AB^2}}=\dfrac{a\sqrt{2}}{2}\)
\(AH\perp\left(SBC\right)\Rightarrow AH\perp HK\Rightarrow\Delta AHK\) vuông tại H
\(sin\widehat{AKH}=\dfrac{AH}{AK}=\dfrac{\sqrt{3}}{2}\Rightarrow\widehat{AKH}=60^0\)