Bài 3: Đường thẳng vuông góc với mặt phẳng
Các câu hỏi tương tự
Cho hình chóp SABC, đáy tam giác ABC vuông tại B. Gọi H là hình chiếu của A lên SB(SA vuông góc (ABC)) a. Chứng minh: BC vuông góc (SAB) B. Gọi I là hình chiếu của B lên AC Chứng minh BI vuông góc (SAC) c. Kẻ AK vuông góc SC tại K, Chứng minh:AH vuông góc SC
Hình chóp tam giác S.ABC có đáy ABC là tam giác vuông tại A và có cạnh bên SA vuông góc với mặt phẳng đáy là (ABC). Gọi D là điểm đối xứng của điểm B qua trung điểm O của cạnh AC. Chứng minh rằng \(CD\perp CA,CD\perp\left(SCA\right)\) ?
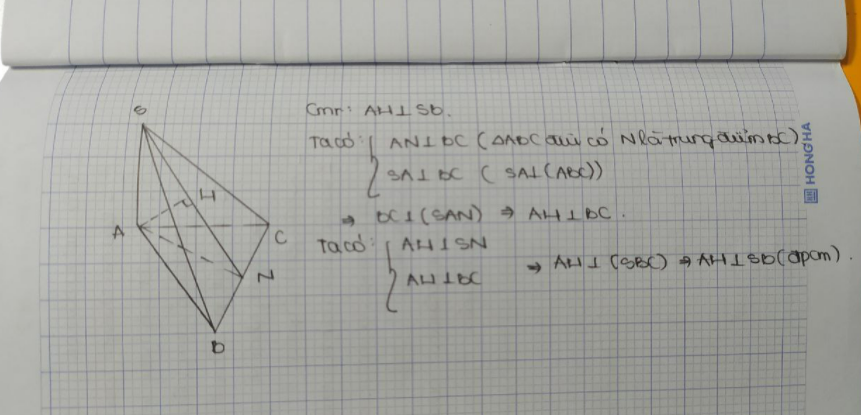
Cho hình chóp s.abc có đáy là tâm giác vuông tại tỉnh B và SA vuông góc (ABC). Gọi M và N lần lượt theo thứ tự là hình chiếu vuông góc của điểm A lên hai cạnh SB và SC. Chứng minh rằng: SC vuông góc (AMN)
Cho hình chóp s.abc có đáy là tâm giác vuông tại tỉnh B và SA vuông góc (ABC). Gọi M và N lần lượt theo thứ tự là hình chiếu vuông góc của điểm A lên hai cạnh SB và SC. Chứng minh rằng: SC vuông góc (AMN) #plssssss
Cho hình chóp tam giác S.ABC , biết rằng SA vuông góc ( ABC ) và tam giác ABC vuông tại B. Gọi M là trung điểm cạnh BC . a ) Xác định hình chiếu vuông góc của S lên ( ABC ) . b ) Xác định hình chiếu vuông góc của đường thẳng SC lên ( ABC ) . c ) Xác định hình chiếu vuông góc của đường thẳng SM lên ( ABC )
d ) Xác định góc của đường thẳng SC và ( ABC ) . e)Xác định góc của đường thẳng SM và ( ABC ) .
Đọc tiếp
Cho hình chóp tam giác S.ABC , biết rằng SA vuông góc ( ABC ) và tam giác ABC vuông tại B. Gọi M là trung điểm cạnh BC . a ) Xác định hình chiếu vuông góc của S lên ( ABC ) . b ) Xác định hình chiếu vuông góc của đường thẳng SC lên ( ABC ) . c ) Xác định hình chiếu vuông góc của đường thẳng SM lên ( ABC )
d ) Xác định góc của đường thẳng SC và ( ABC ) . e)Xác định góc của đường thẳng SM và ( ABC ) .
Cho hình chóp S.ABC có đáy ABC là tam giác cân tại A, điểm I và H lần lượt là trung điểm của AB và BC. Trên đoạn CI và SA lần lượt lấy hai điểm M, N sao cho MC=2MI, NA=2NS. Biết \(SH\perp\left(ABC\right)\), chứng minh \(MN\perp\left(ABC\right)\)
Cho hình chóp S. ABC, đáy \(\Delta ABC\) vuông tại B. \(SA\perp\left(ABC\right)\), B' là hình chiếu của A lên SB; C' là hình chiếu của A lên SC. Tính góc giữa \(\left(BC;\left(SB'C'\right)\right)\). Biết \(AB=a,BC=a\sqrt{3},SA=a\)
Cho hình chóp S.ABC có đáy là tam giác vuông tại B, SA vuông góc với đáy. Hạ AH vuông góc với SB, AK vuông góc với SC.
a, CM các mặt bên của hình chóp là các tam giác vuông.
b, CM tam giác SHK vuông.
c, Gọi D là giao điểm của HK và BC. CM: AC vuông góc với AD.
Mình cần phần c thôi nhé!
cho hình chóp sabc có abc là tam giác vuông tại a, sb vuông (abc) sb=ab. gọi h,i,k lần lượt là trung điểm sa,bc,ab chứng minh ab vuông ih