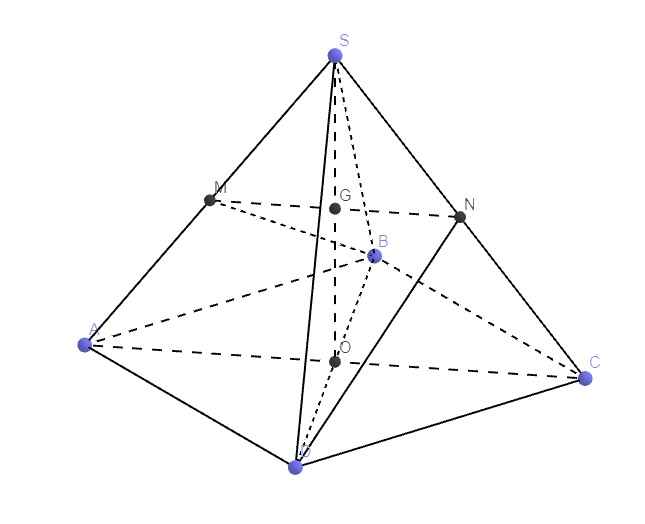
Gọi O là tâm đáy và G là giao điểm của SO và MN
Do MN là đường trung bình tam giác SAC \(\Rightarrow\) G là trung điểm SO
\(\overrightarrow{BO}=\dfrac{1}{2}\overrightarrow{BD}\) ; \(\overrightarrow{OG}=\dfrac{1}{2}\overrightarrow{OS}\) ; \(\overrightarrow{GM}=\dfrac{1}{2}\overrightarrow{NM}=\dfrac{1}{4}\overrightarrow{CA}\) ; \(\overrightarrow{GN}=\dfrac{1}{2}\overrightarrow{MN}=\dfrac{1}{4}\overrightarrow{AC}\)
Ta có:
\(\left\{{}\begin{matrix}\overrightarrow{BM}=\overrightarrow{BO}+\overrightarrow{OG}+\overrightarrow{GM}\\\overrightarrow{DN}=\overrightarrow{DO}+\overrightarrow{OG}+\overrightarrow{GN}\end{matrix}\right.\)
\(\overrightarrow{BM}.\overrightarrow{CN}=0\Rightarrow\left(\overrightarrow{BO}+\overrightarrow{OG}+\overrightarrow{GM}\right)\left(\overrightarrow{CO}+\overrightarrow{OG}+\overrightarrow{GN}\right)=0\)
\(\Leftrightarrow\left(\dfrac{1}{2}\overrightarrow{BD}+\dfrac{1}{2}\overrightarrow{OS}+\dfrac{1}{4}\overrightarrow{CA}\right)\left(\dfrac{1}{2}\overrightarrow{DB}+\dfrac{1}{2}\overrightarrow{OS}+\dfrac{1}{4}\overrightarrow{AC}\right)=0\)
\(\Leftrightarrow-\dfrac{1}{4}BD^2+\dfrac{1}{4}OS^2-\dfrac{1}{4}AC^2=0\) (3 vecto \(\overrightarrow{OS};\overrightarrow{BD};\overrightarrow{CA}\) đôi một vuông góc nên tích vô hướng giữa các cặp đều bằng 0)
\(\Leftrightarrow SO^2=2AC^2\Rightarrow SO=AC\sqrt{2}=2a\)
\(V=\dfrac{1}{3}SO.AB^2=\dfrac{2}{3}a^3\)