Bài 1: Định lý Talet trong tam giác
Các câu hỏi tương tự
cho hình bình hành ABCD. một đường thẳng d cắt AB , BC, BD thứ tự tại M N I. chứng minh rằng : \(\dfrac{AB}{MB}+\dfrac{BC}{BN}=\dfrac{BD}{BI}\)
Cho hình thang ABCD có AB //CD và AB CD. Đường thẳng song song với đáy AB cắt các cạnh bên AD, BC theo thứ tự tại M và N.
Chứng minh rằng :
a) dfrac{MA}{AD}dfrac{NB}{BC}
b) dfrac{MA}{MD}dfrac{NB}{NC}
c) dfrac{MD}{DA}dfrac{NC}{CB}
Hướng dẫn : Kéo dài các tia DA, CB cắt nhau tại E (h.3), áp dụng định lí Ta - let trong tam giác và tính chất của tỉ lệ thức để chứng minh
Đọc tiếp
Cho hình thang ABCD có AB //CD và AB < CD. Đường thẳng song song với đáy AB cắt các cạnh bên AD, BC theo thứ tự tại M và N.
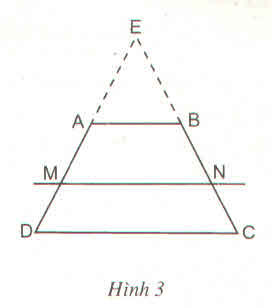
Chứng minh rằng :
a) \(\dfrac{MA}{AD}=\dfrac{NB}{BC}\)
b) \(\dfrac{MA}{MD}=\dfrac{NB}{NC}\)
c) \(\dfrac{MD}{DA}=\dfrac{NC}{CB}\)
Hướng dẫn : Kéo dài các tia DA, CB cắt nhau tại E (h.3), áp dụng định lí Ta - let trong tam giác và tính chất của tỉ lệ thức để chứng minh
Cho hình thang ABCD (AB // CD) và AB < CD. Đường thẳng song song với đáy AB cắt các cạnh bên AD , BC theo thứ tự tại M, N. Chứng minh rằng: a) MA NB AD BC = b) MA NB MD NC = c) MD NC DA CB = Hướng dẫn: Kéo dài các tia DA và CB cắt nhau tại E, áp dụng định lý Ta – lét trong tam giác và tính chất tỉ lệ thức để chứng minh
giúp mik với thanks nhiều nha:))
Cho hình bình hành ABCD. Một đường thẳng qua A cắt tia đối tia BD tại I và cắt tia CB, CD tại H và K.
a) Chứng minh \(\dfrac{AH}{AK}=\dfrac{HB}{AD}\)
b) Hai tỉ số \(\dfrac{AH}{AK}\) và \(\dfrac{AH}{AI}\) bằng những tỉ số nào?
c) Chứng minh \(\dfrac{1}{AI}+\dfrac{1}{AK}=\dfrac{1}{AH}\)
cho hình thang ABCD có AB//CD và AB<CD.Một đường thẳng a song song với các cạnh đấy AB,CD và cắt các cạnh bên AD,BC thứ tự tại M và N.Chứng minh rằng:
a)MA/AD=NB/BC
b)MA/MD=NB/NC
c)MD/AD=NC/BC
cho hình bình hành abcd một đường thẳng đi qua a lần lượt cắt bd ở i bc tại j và cd tại k a) so sánh ib/id và dc/dk b)ia^2=ij.ik c) cmr dc/dk=bi/bc
Cho hình bình hành ABCD. Một đường thẳng qua A lần lượt cắt BD ở I, BC ở J và CD ở K.a. So sánh ID/IBvà IK/IA b. Chứng minh: IA^2= IJ . IK c. Chứng minh:DC/DK= BJ/BC
Cho hình thang ABCD có AB=3cm, CD=5cm (AB//CD). Lấy M,N thuộc AD, BC sao cho MN//AB và \(\dfrac{MA}{MD}=3\). Gọi I là giao điểm của AC và MN.
a) Tính tỉ số \(\dfrac{IA}{IC};\dfrac{NB}{NC}\)
b) Tính MN
Cho ΔABC , trên AB lấy điểm M, trên AC lấy điểm N sao cho \(\dfrac{AM}{AB}=\dfrac{1}{2}và\dfrac{AN}{AC}=\dfrac{1}{2}\)
a) Chứng minh MN//BC
b) Trung tuyến AI cắt MN tại K. Chứng minh : K là trung điểm MN










