Bài 1: Định lý Talet trong tam giác
Các câu hỏi tương tự
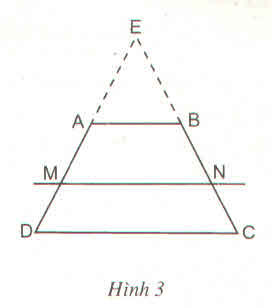
Cho hình thang ABCD có AB //CD và AB CD. Đường thẳng song song với đáy AB cắt các cạnh bên AD, BC theo thứ tự tại M và N.
Chứng minh rằng :
a) dfrac{MA}{AD}dfrac{NB}{BC}
b) dfrac{MA}{MD}dfrac{NB}{NC}
c) dfrac{MD}{DA}dfrac{NC}{CB}
Hướng dẫn : Kéo dài các tia DA, CB cắt nhau tại E (h.3), áp dụng định lí Ta - let trong tam giác và tính chất của tỉ lệ thức để chứng minh
Đọc tiếp
Cho hình thang ABCD có AB //CD và AB < CD. Đường thẳng song song với đáy AB cắt các cạnh bên AD, BC theo thứ tự tại M và N.
Chứng minh rằng :
a) \(\dfrac{MA}{AD}=\dfrac{NB}{BC}\)
b) \(\dfrac{MA}{MD}=\dfrac{NB}{NC}\)
c) \(\dfrac{MD}{DA}=\dfrac{NC}{CB}\)
Hướng dẫn : Kéo dài các tia DA, CB cắt nhau tại E (h.3), áp dụng định lí Ta - let trong tam giác và tính chất của tỉ lệ thức để chứng minh
Cho hình bình hành ABCD. Vẽ tia Ax cắt đường chéo BD ở I, cắt tia BC ở J và cắt tia DC ở K.
a) Theo định lý Talet thì tỉ số ID/IB bằng với những tỉ số nào? Chứng minh IA2 = IJ.IK
b) Hai tỉ số AI/AJ và AI/AK bằng tỉ số nào trên đường chéo BD? Chứng minh 1/AJ + 1/AK = 1/AI
Cho hình thang ABCD, AB // BC. I là giao của hai đường chéo. Qua I vẽ đường thẳng song song với hai đáy cắt AD tại E , BC tại F.
a, Chứng minh IE = IF
b, Chung minh \(\dfrac{1}{AB}+\dfrac{1}{CD}=\dfrac{1}{IE}\)
c, Chứng minh \(\dfrac{2}{EF}=\dfrac{1}{AB}+\dfrac{1}{CD}\)
cho hình bình hành ABCD. một đường thẳng d cắt AB , BC, BD thứ tự tại M N I. chứng minh rằng : \(\dfrac{AB}{MB}+\dfrac{BC}{BN}=\dfrac{BD}{BI}\)
Cho hình bình hành ABCD. Qua A vẽ tia Ax cắt BD tại M, cắt BC tai N và cắt CD ở K
a, So sánh tỉ số giữa \(\dfrac{MB}{MD}\) và \(\dfrac{MA}{MK}\); \(\dfrac{MB}{MD}\) và \(\dfrac{MN}{MA}\)
b, Chứng minh rằng : MA2= MN.MK
Cho widehat{xOy} khác góc bẹt.Đường thẳng a cắt các tia Ox;Oy theo thứ tự tại A;B sao cho dfrac{1}{AO}+dfrac{1}{BO}k (k là hằng số).
a)Chứng minh đường thẳng a luôn đi qua một điểm cố định K.
b)Dựng đường thẳng a sao cho tổng dfrac{1}{AK}+dfrac{1}{BK}đạt giá trị lón nhất.
Hãy giúp tôi....
Đọc tiếp
Cho \(\widehat{xOy}\) khác góc bẹt.Đường thẳng \(a\) cắt các tia \(Ox;Oy\) theo thứ tự tại \(A;B\) sao cho \(\dfrac{1}{AO}+\dfrac{1}{BO}=k\) (\(k\) là hằng số).
a)Chứng minh đường thẳng \(a\) luôn đi qua một điểm cố định \(K\).
b)Dựng đường thẳng \(a\) sao cho tổng \(\dfrac{1}{AK}+\dfrac{1}{BK}\)đạt giá trị lón nhất.
Hãy giúp tôi....
Cho hình thang ABCD (AB//CD),AC cắt BD tại O.Từ O kẻ đường thẳng // AB cắt AD,BC tại I,K.
Cminh:\(\dfrac{AI}{AD}\)=\(\dfrac{BK}{BC}\)
b) O là trung điểm IK
MỌI NGƯỜI GIÚP MÌNH NHAAA
Cho tam giác ABC vuông tại A ( AB AC ) . Kẻ AH vuông góc với BC tại H. Qua B kẻ đường thẳng vuông góc với AB , cắt đường thẳng AH tại D. Gọi tia AB và tia CD cắt nhau tại E. BE DE a ) Chứng minh : BA DC b ) Qua E kẻ đường thẳng song song với AC , đường thẳng này lần lượt cắt các đường thăng AD , BC tại I , K. Chứng minh : El EK ; c ) Gọi N là giao điểm của EH và AC ; Gọi Q là giao điểm của DN và BC ; Gọi P là giao điểm của BN và AD . Chúng minh : NA NC và PQ // BD ; d ) Gọi G là giao điểm của...
Đọc tiếp
Cho tam giác ABC vuông tại A ( AB < AC ) . Kẻ AH vuông góc với BC tại H. Qua B kẻ đường thẳng vuông góc với AB , cắt đường thẳng AH tại D. Gọi tia AB và tia CD cắt nhau tại E. BE DE a ) Chứng minh : BA DC b ) Qua E kẻ đường thẳng song song với AC , đường thẳng này lần lượt cắt các đường thăng AD , BC tại I , K. Chứng minh : El = EK ; c ) Gọi N là giao điểm của EH và AC ; Gọi Q là giao điểm của DN và BC ; Gọi P là giao điểm của BN và AD . Chúng minh : NA = NC và PQ // BD ; d ) Gọi G là giao điểm của đường thẳng AQ và CD . Qua Q kẻ đường thẳng song song với CE , cắt đường thẳng AC tại T. Chứng minh PT LAD
Cho ΔABC , trên AB lấy điểm M, trên AC lấy điểm N sao cho \(\dfrac{AM}{AB}=\dfrac{1}{2}và\dfrac{AN}{AC}=\dfrac{1}{2}\)
a) Chứng minh MN//BC
b) Trung tuyến AI cắt MN tại K. Chứng minh : K là trung điểm MN











