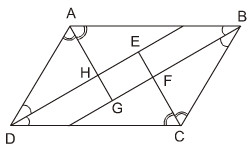
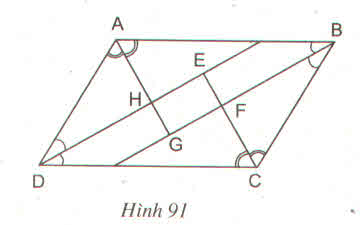
Ta có :
(hình bình hành)
(gt)
(gt)
=>
Mà :
=>
=> DM // BF ( ở vị trí đồng vị)
Hay : EH // FG
cmtt, ta có : GH // EF
=> EFGH là hình bình hành (1).
(hình bình hành)
(gt)
(gt)
=>
=> (tổng 3 góc của tam giác AHD)
=> (đối đỉnh) (2).
Từ (1) và (2) => EFGH là hình chữ nhật