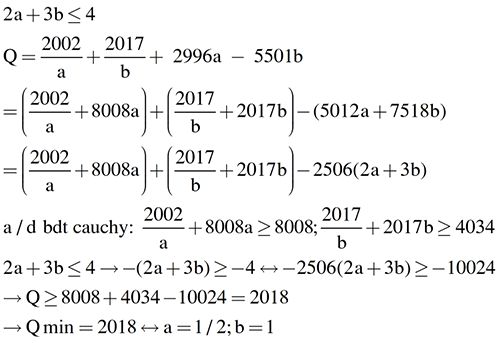Ta có:
\(Q=\dfrac{2002}{a}+\dfrac{2017}{b}+2996a-5501b\)
\(=\left(\dfrac{2002}{a}+8008a\right)+\left(\dfrac{2017}{b}+2017b\right)-\left(5012a+7518b\right)\)
\(=\left(\dfrac{2002}{a}+8008a\right)+\left(\dfrac{2017}{b}+2017b\right)-2506\left(2a+3b\right)\)
Áp dụng BĐT Cauchy cho hai số không âm ta có:
\(\dfrac{2002}{a}+8008a\ge2\sqrt{\dfrac{2002}{a}.8008a}=2.4004=8008\) (1)
\(\dfrac{2017}{b}+2017b\ge2\sqrt{\dfrac{2017}{b}.2017b}=2.2017=4034\) (2)
Có \(2a+3b\le4\Rightarrow-\left(2a+3b\right)\ge-4\Rightarrow-2506\left(2a+3b\right)\ge-10024\)(3)
Từ (1), (2) và (3) \(\Rightarrow Q\ge8008+4034-10024=2018\)
Dấu '=' xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2002}{a}=8008a\\\dfrac{2017}{b}=2017b\\2a+3b=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b=1\end{matrix}\right.\)
Vậy,...
![]()