Question

Cho góc xAy=60 độ, vẽ tia phân giác Az của góc đó. Từ một điểm B trên Ax vẽ đường thẳng song song với Ay cắt Az tại C. Vẽ \(BH\perp Ay,CM\perp Ay,BK\perp AC\). Chứng minh rằng:

a) K là trung điểm của AC

b) \(BH=\frac{AC}{2}\)

c) Tam giác KMC đều

Answer 1

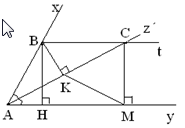
a) Vì \(Az\) là tia phân giác của \(\widehat{BAM}\left(gt\right)\)

=> \(K\) là trung điểm của \(AC.\)

b) Vì \(K\) là trung điểm của \(AC\left(cmt\right).\)

=> \(AK=\frac{1}{2}AC\) (tính chất trung điểm).

Vì \(Az\) là tia phân giác của \(\widehat{BAH}\left(gt\right)\)

Mà \(AK=\frac{1}{2}AC\left(cmt\right)\)

=> \(BH=\frac{1}{2}AC.\)

Hay \(BH=\frac{AC}{2}.\)

c) Ta có:

Answer 2

a. Ta có: BC//Ay(gt)\(\Rightarrow\widehat{BCA}=\widehat{MAC}\) (2 góc so le trong)

Mà: \(\widehat{MAC}=\widehat{CAB}=\frac{60^o}{2}=30^o\) ( vì AC là tia phân giác \(\widehat{xAy}\) )

\(\Rightarrow\widehat{BAC}=\widehat{BCA}\Rightarrow\Delta BAC\) cân tại B

Xét \(\Delta BAC\) cân tại B, có: BK là đường cao

\(\Rightarrow\) BK là đường trung tuyến

\(\Rightarrow K\) là trung điểm AC

b. Xét \(\Delta HAB\) có: \(\widehat{HBA}=180^o-90^o-60^o=30^o\)

Mà: \(\widehat{KAB}=30^o\left(cmt\right)\)

\(\Rightarrow\widehat{HBA}=\widehat{KAB}\left(=30^o\right)\)

Xét \(\Delta KAB\left(\widehat{K}=90^o\right)\) và \(\Delta HBA\left(\widehat{H}=90^o\right)\) có:

\(AB\) chung

\(\widehat{HBA}=\widehat{KAB}\left(cmt\right)\)

\(\Rightarrow\Delta KAB=\Delta HBA\left(ch-gn\right)\)

\(\Rightarrow BH=AK\) ( 2 cạnh tương ứng )

Mà: \(AK=\frac{AC}{2}\)

\(\Rightarrow BH=\frac{AK}{2}\)

Answer 3

!