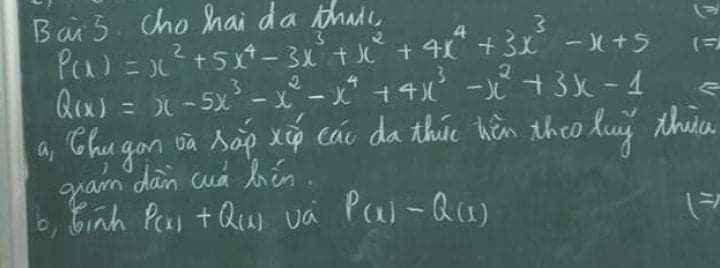ta có
\(A\left(x\right)=x^3-\left(x^2+2x\right)\\ A\left(x\right)=x^3-x^2+2x\)
\(B\left(x\right)=2x^4-3x^3+x^2-2x^4-3x^2\\ =\left(2x^4-2x^4\right)-3x^3+\left(x^2-3x^2\right)\\ B\left(x\right)=-3x^3-2x^2\)
a/ ta có
\(M\left(x\right)-A\left(x\right)=B\left(x\right)\rightarrow M\left(x\right)=B\left(x\right)+A\left(x\right)\)
\(\rightarrow M\left(x\right)=A\left(x\right)+B\left(x\right)=x^3-x^2+2x+\left(-3x^3\right)-2x^2\)
\(=\left(x^3-3x^3\right)+\left(-x^2-2x^2\right)+2x\\ \rightarrow M\left(x\right)=-2x^3-3x^2+2x\)
b/
ta có
\(N\left(x\right)+A\left(x\right)=B\left(x\right)\rightarrow N\left(x\right)=B\left(x\right)-A\left(x\right)\)
\(\rightarrow N\left(x\right)=B\left(x\right)-A\left(x\right)=\left(-3x^3-2x^2\right)-\left(x^3-x^2+2x\right)\)
\(=-3x^3-2x^2-x^3+x^2-2x\\ =\left(-x^3-3x^3\right)+\left(x^2-2x^2\right)-2x\\ \rightarrow N\left(x\right)=-4x^3-x^2-2x\)
c/
ta có
\(P\left(x\right)+B\left(x\right)=A\left(x\right)\rightarrow P\left(x\right)=A\left(x\right)-B\left(x\right)\)
\(\rightarrow P\left(x\right)=A\left(x\right)-B\left(x\right)=\left(x^3-x^2+2x\right)-\left(-3x^3-2x^2\right)\)
\(=x^3-x^2+2x+3x^3+2x^2\\ =\left(x^3+3x^3\right)+\left(2x^2-x^2\right)+2x\\ \rightarrow P\left(x\right)4x^3+x^2+2x\)






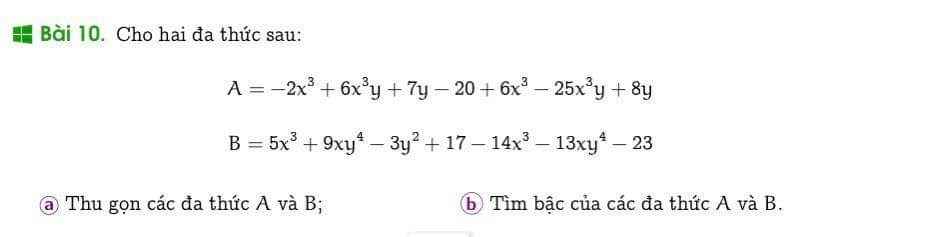 Giúp mik vớii ( chi tiết nếu đc ạ)
Giúp mik vớii ( chi tiết nếu đc ạ) 

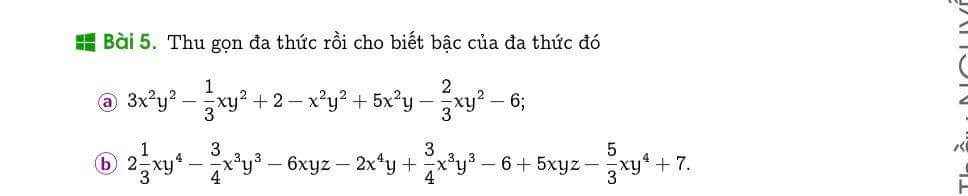 Cứu mik với, mik cảm ơn
Cứu mik với, mik cảm ơn